摘要
線索二叉樹概念
線索二叉樹當用二叉鍊表作為二叉樹的存儲結構時，因為每個結點中只有指向其左、右兒子結點的指針，所以從任一結點出發只能直接找到該結點的左、右兒子。在一般情況下靠它無法直接找到該結點在某種遍歷序下的前驅和後繼結點。如果在每個結點中增加指向其前驅和後繼結點的指針，將降低存儲空間的效率。
我們可以證明：在n個結點的二叉鍊表中含有n+1個空指針。因為含n個結點的二叉鍊表中含有2n個指針，除了根結點，每個結點都有一個從父結點指向該結點的指針，因此一共使用了n-1個指針，所以在n個結點的二叉鍊表中含有n+1個空指針。
因此可以利用這些空指針，存放指向結點在某種遍歷次序下的前驅和後繼結點的指針。這種附加的指針稱為線索，加上了線索的二叉鍊表稱為線索鍊表，相應的二叉樹稱為線索二叉樹(ThreadedBinaryTree)。根據線索性質的不同，線索二叉樹可分為前序線索二叉樹、中序線索二叉樹和後序線索二叉樹三種。
線索二叉樹結構
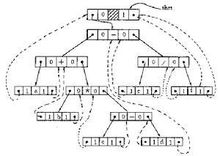
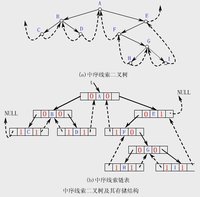
例如圖(a)是一棵中序線索二叉樹，它的線索鍊表如圖(b)所示。
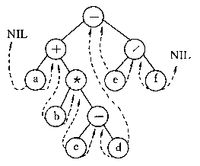線索二叉樹(a)
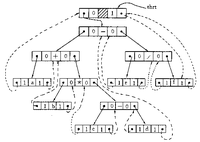線索二叉樹(b)
圖(b)中，在二叉樹的線索鍊表上增加了一個頭結點，其LeftChild指針指向二叉樹的根結點，其RightChild指針指向中序遍歷時的最後一個結點。另外，二叉樹中依中序列表的第一個結點的LeftChild指針，和最後一個結點的RightChild指針都指向頭結點。這就像為二叉樹建立了一個雙向線索鍊表，既可從第一個結點起，順著後繼進行遍歷，也可從最後一個結點起順著前驅進行遍歷。
如何線上索二叉樹中找結點的前驅和後繼結點？以圖13的中序線索二叉樹為例。樹中所有葉結點的右鏈是線索，因此葉結點的RightChild指向該結點的後繼結點，如圖13中結點"b"的後繼為結點"*"。當一個內部結點右線索標誌為0時，其RightChild指針指向其右兒子，因此無法由RightChild得到其後繼結點。然而，由中序遍歷的定義可知，該結點的後繼應是遍歷其右子樹時訪問的第一個結點，即右子樹中最左下的結點。例如在找結點"*"的後繼時，首先沿右指針找到其右子樹的根結點"-"，然後沿其LeftChild指針往下直至其左線索標誌為1的結點，即為其後繼結點(在圖中是結點"c")。類似地，在中序線索樹中找結點的前驅結點的規律是：若該結點的左線索標誌為1，則LeftChild為線索，直接指向其前驅結點，否則遍歷左子樹時最後訪問的那個結點，即左子樹中最右下的結點為其前驅結點。由此可知，若線索二叉樹的高度為h，則在最壞情況下，可在O(h)時間內找到一個結點的前驅或後繼結點。在對中序線索二叉樹進行遍歷時，無須像非線索樹的遍歷那樣，利用遞歸引入棧來保存待訪問的子樹信息。
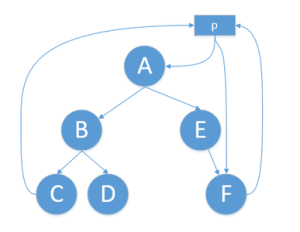
對一棵非線索二叉樹以某種次序遍歷使其變為一棵線索二叉樹的過程稱為二叉樹的線索化。由於線索化的實質是將二叉鍊表中的空指針改為指向結點前驅或後繼的線索，而一個結點的前驅或後繼結點的信息只有在遍歷時才能得到，因此線索化的過程即為在遍歷過程中修改空指針的過程。為了記下遍歷過程中訪問結點的先後次序，可附設一個指針pre始終指向剛剛訪問過的結點。當指針p指向當前訪問的結點時，pre指向它的前驅。由此也可推知pre所指結點的後繼為p所指的當前結點。這樣就可在遍歷過程中將二叉樹線索化。對於找前驅和後繼結點這二種運算而言，線索樹優於非線索樹。但線索樹也有其缺點。在進行插人和刪除操作時，線索樹比非線索樹的時間開銷大。原因在於線上索樹中進行插人和刪除時，除了修改相應的指針外，還要修改相應的線索。
