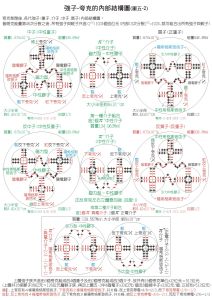
分類
強子按其組成夸克的不同，強子還可以分為：
1、重子(baryon)：重子由三個夸克或三個反夸克組成，它們的自鏇總是半數的，也就是說，它們是費米子。它們包括人們比較熟悉的組成原子核的質子和中子和一般鮮為人知的超子（Hyperon,比如Δ、Λ、Σ、Ξ和Ω），這些超子一般比核子重，而且壽命非常短。
2、介子(meson)：介子由一個夸克和一個反夸克組成，它們的自鏇是整數的，也就是說，它們是玻色子。介子有許多種。在高空射線與地球空氣相互作用時會產生介子。
其它很稀有和奇怪的強子。
由多於三個但單數的夸克或反夸克組成類似重子的強子。
由多於一對夸克-反夸克對組成的類似介子的強子。
完全由膠子組成的粒子。
介子的自鏇（粒子的固有角動量）量子數為整數（也稱玻色子）
重子的自鏇量子數為半整數。(也屬於費米子）
質子的自鏇量子數為半整數1/2，並且參與強相互作用。所以質子屬於強子的一種。
目前發現的所有強子都滿足蓋爾曼-西島關係，即：Ｓ＝２（Ｑ-Ｉ３）-Ｂ，Ｓ是奇異數，Ｑ是電荷，Ｉ３是同位鏇，Ｂ為重子數。
構成
強子的構成是粒子物理的基本問題之一。在樸素夸克模型中，強子具有$\barqq$(介子)和$qqq$(重子)構成。但是這種簡單的構成正受到來自實驗的嚴峻挑戰。無論是越來越多的無法歸類的強子態，還是具有無法為樸素夸克模型所容許量子數的介子的發現，都暗示有超越樸素夸克模型構成的新強子存在。膠球、多夸克態和混雜子是三種可能的新強子構造，它們分別是膠子、多夸克以及夸克與膠子的束縛態。本文將研究這些新強子的性質。首先是所採用的研究方法的介紹，由於我們採用QCD求和規則作為我們的主要理論框架，因此對於瞬子物理我們主要採用一種易於使用到QCD求和規則框架內的半唯象方法，即單瞬子近似。
對於某些特定新強子性質的研究。在考慮了直接的瞬子效應後，我們在QCD求和規則的框架內研究了$0^{++}$膠球的質量問題。結果顯示在考慮了瞬子效應後，膠球的質量被大大降低。之後我們考慮瞬子效應在標量膠球衰變中的作用。我們發現由於非微擾效應，標量膠球衰變過程中$SU(3)_f$對稱性是被很好保持的。我們也考慮了標量膠球的四夸克衰變與兩夸克衰變寬度之比。與普通介子衰變相比，我們預言標量膠球衰變會有較大的多強子末態分支比。首先構造了兩個典型的$1^{-+}$分子四夸克態，利用考慮瞬子效應修正後的QCD求和規則研究它們的質量問題。我們發現我們的模型可以在1.4GeV附近容納兩個不同的$1^{-+}$四夸克介子。接著構造具有Diquark結構和分子態結構的四夸克態，並研究了它們的衰變方式。在已有的$1^{-+}$和$0^{++}$混雜子質量的求和規則中考慮直接的瞬子效應，研究瞬子在其中所起的作用，並給出較穩定的$0^{++}$膠球的質量預言。
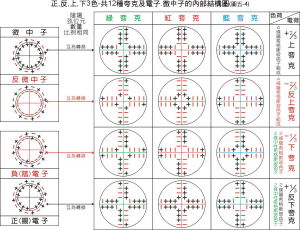夸克(層子)與輕子間的對稱性-結構圖1964年，美國科學家蓋爾曼等人提出“夸克模型”。他們認為，所有的強子都是由若干種叫做“夸克”的更深層次的粒子組成。西方人將這些粒子稱為“夸克”，中國人則常常又稱它們為“層子”。顧名思義，層子是相對電子、質子、中子這些基本粒子來說的，它屬於“下一層次的粒子”。蓋爾曼等人認為夸克帶“分數電荷”，它們被禁閉在強子內部，不能脫離強子自由運動。
夸克模型出現之後，又有人提出夸克是物質分割的極限。因為夸克被禁閉在強子內部，本身也無法直接觀察。然而，對大自然的好奇心，促使人們對夸克是否還有“內部結構”這個問題產生濃厚的興趣。目前的跡象表明，夸克和輕子可能是由某些更為基本的粒子所組成，夸克和輕子之間具有極大的對稱性。根據目前的理論，夸克可分為三代，每代有兩種（不計反夸克），它們分別是（u,d）、（c,s）和（t,b）。輕子也有三代，每代也有兩種。如此多的粒子表明，即便夸克和輕子，也不可能是物質分割的“最小單元”。
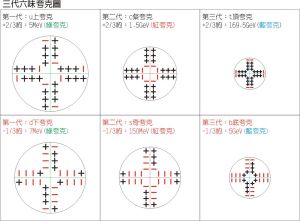三代夸克圖但是從1964年至今，人們還沒有“看到”過夸克的真實面目。在蓋爾曼提出的夸克理論中，他假設存在三種夸克。他用這三種夸克及它們的反粒子來說明微觀粒子構成的模型，取得了很大的成功。但是，由於物理學家至今還不能使夸克脫離其他微觀粒子而獨立存在，它只能像犯了錯誤而被關禁閉的士兵那樣，被幽禁在微觀粒子中。所以，“夸克禁閉”成了當今粒子物理學的難題之一，這對哲學中關於物質無限可分的觀點，也是一次嚴峻的挑戰。
近半個世紀以來，物理學家為了尋找自由夸克，絞盡了腦汁。每當一台新的高能加速器建成以後，首要的任務之一就是試圖找到夸克。有的物理學家把微觀粒子想成一隻口袋，夸克永遠被裹在這隻口袋裡——在這口袋的小範圍內，它可以自由飛翔，但決不許脫離這個口袋。就是這個神秘的口袋，似乎要把夸克同外界永遠隔離開來。也有的物理學家把微觀構想成一口半徑很小又很深的“井”，夸克過的就是這種“坐‘井’觀天”的生活。在“井”里它們都相當自由，運動速度也不快，可就是跑不出去。人們必須提供極大的能量，才能把它從“井”底拉出來。但是目前人們還沒有辦法產生這么大的能量，使夸克獲得“解放”。
既然不能直接找到自由夸克，一些物理學家就改變了策略，企圖間接地搜尋它。因為根據理論推測，夸克帶有所謂的“分數電荷”，這使物理學家看到了一線希望。他們認為只要找到了“分數電荷”的攜帶者，那也許它就是夸克的化身了。因此物理學家在粒子加速器、隕石、月球、地下深井和海底等許多地方“張羅織網”，到處尋找具有“分數電荷”的粒子。
目前探測夸克結構和輕子結構的實驗都在進行中，但未取得進展。考慮到原子和原子核的線度相差10萬倍，因而可以預言夸克的結構最多只能在10-20米的尺度上顯示出來；但目前的實驗只能探測到10-17米的線度，因而夸克究竟是否有“內部結構”，至今還是一個謎。
結構的層子模型
強子強子結構的層子模型(以下簡稱“層子模型”)是在1965年9月到1966年6月之間完成的。當時的研究背景是這樣的：在電子、質子、中子發現之後，人們普遍認為它們是構成物質的終極單元，稱之為“基本粒子”。隨著介子和超子在20世紀40到50年代的陸續發現，基本粒子的家族迅速擴大，這些粒子絕大部分是強作用粒子，簡稱強子。很難想像這么多的強子都是基本粒子。1955年日本物理學家坂田提出了一個結構模型：強子中只有質子、中子和超子三種是基礎的粒子，由它們構成其他所有的強子。坂田模型存在一系列困難，但是所提出的強子具有內部結構的思想是正確的。1964年美國物理學家蓋爾曼改造了坂田模型，提出了“夸克模型”，認為強子是由三種具有SU(3)對稱性的組分構成的，他把這些組分稱為夸克。
到了1965年，基本粒子表中粒子的數目已經可以與周期表中元素的數目相比，其中重子的自鏇可以高達11/2，並且實驗上關於核子的電磁形狀因子的測量說明以前被認為是基本粒子的核子具有一定的大小和空間結構。這些事實說明了兩點，一是“基本粒子”並不基本，二是強子有著內部結構。坂田模型和夸克模型都是關於強子結構的科學構想，有待於進一步發展為強子結構的科學理論。但是在當時發展強子結構的理論有困難，因為不知道在強子內部是否有新的力學規律在起作用，不知道強相互作用的具體形式，不知道處理強相互作用的數學方法，所以在結構模型中還只限於討論由對稱性能夠得出的強子分類、新粒子預言和諸如質量、自鏇、電荷、磁矩等靜態性質。進一步的發展必須超出對稱性的範疇，引入動力學起作用的因素。
在當時已知的最高能量下，物理實驗結果表明量子數、本徵值、幾率波這些概念仍然有效，也就是說在強子內部的小尺度範圍中，用波函式描述狀態、用算符描述物理量的基本概念和方法仍然有效。於是他提出引入強子內部的結構波函式來描述強子內部結構的狀態，至於決定波函式的力學規律和運動方程等則留待以後去討論，一些嚴格的物理要求如相對論洛倫茲協變性和內部對稱性等已經大大限制了波函式可能具有的形式。強子的組成及遵從的對稱性是否取夸克模型或坂田模型的其他變種，所以後來按錢三強的建議把強子的組分粒子稱為“層子”，表示物質結構許多層次中的一個層次的意思。在引入波函式以描述運動著的強子時，他認為應當區分描述內部運動和整體運動的兩個概念。通過對已知實驗數據的分析，他提出層子在強子內部的運動速度遠小於光速，是非相對論性的，雖然強子的整體運動可以是相對論性的。
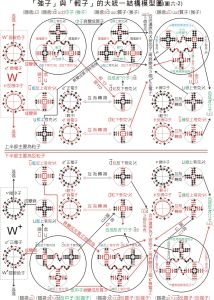夸克及輕子互相衰變-結構圖這樣，可以在強子的靜止坐標系中定出非相對論性的結構波函式，然後通過洛倫茲變換得到作自由運動的強子的波函式。在討論強子發生轉化的過程時，朱洪元引入始態和終態強子結構波函式的重疊積分的概念和具有特定的對稱性的強子構成組分(層子)之間的相互作用來計算躍遷矩陣元，用以統一地描述一系列強子的轉化過程。在這些概念和方法的基礎上，由錢三強大力支持，朱洪元領導的粒子理論研究集體系統地研究了強子的力學、電磁及幾何等靜態性質，以及強子的電磁衰變、弱衰變、強衰變等動態過程。在九個月里，他們發表了46篇科學論文，得到了一系列理論結果，其中許多和實驗結果相符合。有一些當時沒有實驗數據，在後來才得到實驗的證實。也有一些理論結果與實驗不合，有待後來的實驗和理論工作的新進展來解決。
“層子模型”是強子結構研究的一個重要開拓，它是在層子之間的動力學理論提出來之前的一個方向性的系統工作。這個理論中提出的強子內部結構波函式和波函式的重疊積分的概念沿用至今，隨著層子間強相互作用的動力學理論的建立，它們越來越細緻地被確定下來。在1966年北京亞太科學討論會上，巴基斯坦諾貝爾物理學得主薩拉姆高度評價了這項工作。很可惜，朱洪元和中國粒子物理學家在理論上一個很好的開頭被隨後十年的大破壞所打斷。
多重數分布的質量效應
強子多重數分布的研究，從KNO標度算起，已有30多年的歷史。動量分布的Feynman楊標度被破壞後由平均標度代替。重整化群方程能夠證明KNO標度,而且可得到多重數與非彈性度服從Kendall標度分布。KNO標度的理論基礎是重整化群，是［C‖O］類半群對稱性。強子動量·多重數關聯(S1/2=22～900GeV)的研究表明：粒子·粒子碰撞產生3個發射源，a+b→NJ0+NJ1+NJ2強子；由此確定了基本強子發射源的物理性質(UAl數據,TASSO數據)。在這些研究的基礎上，就可以討論多重數分布對強子質量的依賴了。多重數N被定義為末態強子的總和，其閾能(末態總質量)EN=mπNπ+mкNк+2mрNр+…，顯然是重要的。多重數分布同強子質量產生有關。
目前，強子動量·多重數關聯(ｓ＝22～900ＧｅＶ)的研究表明：粒子·粒子碰撞產生3個強子發射源，ａ＋ｂ→ＮＪ0＋ＮＪ１＋ＮＪ2，強子多重數Ｎ＝ＮＪ0＋ＮＪ１＋ＮＪ2，並由此確定了基本強子發射源的物理性質(UAI數據，TASSO數據)，對NA22的π介子海鷗效應(Seagulleffects)的詳細分析，揭示出3個發射源的運動學與動力學結構，確定了J1與J2的相對論都卜勒(Doppler)效應。近年來的CERN(NA22)實驗研究又指出，不用質量與電荷證認數據，而得出的動力學結論是不完全的。為此，在這些研究的基礎上，才能討論多重數分布對強子質量的依賴性。現在用質量與電荷證認數據來改進多重數分布的研究，從而得出動力學結論。
1、Bose強子的倒易統計起伏
電荷強子多重數Ｎ＝Ｎπ＋Ｎｋ＋Ｎｐ＋Ｎ＋…，在質心能量ｓ＝4～1800ＧｅＶ的區域，π±介子與Ｋ±介子占85%～95%的比率。因此，可近似考慮Bose強子數NB=Nπ+NK.Bose強子平均多重數〈NB〉滿足重整化群方程，即
Ｄ<ＮＢ>＝2γＢ（ｇＲ）Ｄ2ＮＢ（1）
倒易統計起伏αＢ＝<ＮＢ>2／Ｄ2ＮＢ，結合(1)式我們有－Ｄ1<ＮＢ>＝1αＢ2γＢ（ｇＲ）（2）
利用CERN-ISR數據(1978)，UA5數據(Ｐｓ=540GeV，1982)等資料，我們得到強子·強子碰撞經驗公式為<ｍ>＝ｍπ±·ｅｘｐ［0.052／αｓ］（3）
這裡αs是QCD(味數nf=4)跑動耦合常數，αｓ＝0.48／ｌｎ（ｓ／ΛＱＣＤ），ΛＱＣＤ＝2ｍπ±。對於e+e-碰撞(３)式變為<ｍ>＝ｍπ±·（14ｅｘｐ［0.052／αｓ］）(4)
這就是說，e+e-碰撞比Ｐ碰撞多產生ｍπ±/4的質量(ｓs=3～10GeV)。Bose強子平均質量<ｍＢ>＝ｍπ±·ｅｘｐ［0.045／αｓ］（ｓ=3GeV～20TeV)。只考慮π±與Ｋ±介子，Bose強子倒易統計起伏為
αＢ＝<ＮＢ>2<Ｎ2Ｂ>－<ＮＢ>2（5）
則αＫ＝απ<ｍＢ>－ｍπＭＫ－<ｍＢ>（6）
αＢ＝απ（ＭＫ－ｍπＭＫ－<ｍＢ>）2（7）
這裡απ與αＫ分別是π±介子與Ｋ±介子的倒易統計起伏。α０π＝(1.27±0.09)２是比較精確的實驗值，其Ｎ±π的基本強子發射源中的分布為<Ｎπ>σＴｄσπｄＮπ＝
24γＢ－１／２Γ（3／2－4γＢ）（βπＮπ<Ｎπ>）1＋νＫν（βπＮπ<Ｎπ>）(8)
這裡βπ≈2［1－2γＢ－（ｇＲ）］，ν＝1／2－4γＢ（ｇＲ），由Hankel積分公式<Ｎ2π><Ｎπ>＝3／2Γ（2－4γＢ）·［Γ（3／2－4γＢ）Γ（3／2）］2·Γ（5／2－4γＢ）Γ（5／2）（9）
再利用黎曼ζ(q，x)函式與Γ(x)函式的關係，可算出αＪ±π≈2［1－5／2γＢ（ｇＲ）］(10)
式(10)是基本強子發射源的倒易統計起伏。對於3個源(J0，J1，J2），Ｎπ＝ＮＪ０＋ＮＪ１＋ＮＪ2，若J1與J2相同，則有α±π≈αｊ±π［1－（<ＮＪ><Ｎ±π>）］2(11)
再由(7)式，我們最後得αＢ≈α±π（1＋δ<ｍＢ>ＭＫ）2(12)
這裡δ<ｍＢ>＝<ｍＢ>－ｍπ，於是我們可得到：量子場反常維度－γＢ（ｇＲ）＝0.045，δmp=119MeV，2<ＮＪ１>=0.96±0.02。
2、高階積分關聯的質量效應
趙樹松教授曾證明απ滿足蘭道(Landau)不等式，指出αｍａｘπ＝4，這對積分關聯是很強的限制。積分關聯
ｆ2（ｇＲ，<ｍＢ>）＝Ｄ2ＮＢ－<ＮＢ>＝（1αＢ<ＮＢ>－1）·<ＮＢ>(13)
表達式(13)的結果與NA22數據、NA9數據（μｐ）及W21數據（ｐ，ｖｐ）相符合。π+P與K+P碰撞產生Ｋ±的介子平均數分別為(HEN-316/1988)<ＮＫ±>＝0.420±0.015（Ｋ＋Ｐ），<ＮＫ±>＝0.252±0.007（π＋Ｐ）。由(12)式我們有
αＢ（Ｋ＋Ｐ）αＢ（πＰ）≈1＋1ＭＫ［（δ<ｍＢ（Ｋ＋）>－（δ<ｍＢ（π＋）>）］(14)
其平均質量差（δ<ｍＢ（Ｋ＋）>）－（δ<ｍＢ（π＋）>）＝ＭＫ<ＮＢ>δ<ＮＫ±>(15)
這裡δ<ＮＫ±>＝0.168±0.022(Ｋ＋Ｐ碰撞與π＋Ｐ碰撞的Ｋ±介子平均數之差）。具體值為：αＢ（Ｋ＋Ｐ）／αＢ（π＋Ｐ）＝1.020±0.004，這樣Ｋ＋Ｐ數據ｆ2（ｇＫ，<Ｎ>Ｂ）＝0，ｓ＝7.75ＧｅＶ，π＋Ｐ數據ｆ2（ｇＫ，<Ｎ>Ｂ）＝0，ｓ＝7.07ＧｅＶ，由此實驗質量效應得到說明。
奇斜度(skewness)的定義為γ１（ｇＲ，<ｍＢ>）＝<(ＮＢ－<ＮＢ>）3>（<Ｎ2Ｂ>－<ＮＢ>2）3／2(16)
這裡，<(ＮＢ－<ＮＢ>）3>＝<Ｎ3Ｂ>－3<Ｎ2Ｂ>／，<ＮＢ>2＋2<ＮＢ>3，於是我們有γ1（ｇＲ<ｍＢ>）＝α3／2Β［<Ν３Β><ΝΒ>3－3αΒ－1］(17)
由ＮＢ＝ＮＪＢ＋ＮＪ，將式(17)中的<Ｎ3Ｂ>展開，考慮到(7)與(11)式，再令αＪＢ＝（<(ＮＪＢ）2>－<ＮＪＢ>）／Ｄ2ＮＪＢ，經整理可得<Ｎ3Ｂ><ＮＢ>3＝<（ＮＪＢ）3><ＮＢ>3［1－3<ＮＪ><ＮＢ>（1－3<ＮＪ><ＮＢ>）＋3<ＮＪ><ＮＢ>（1－<ＮＪ><ＮＢ>）×（1＋1αＪＢ）］(18)
這裡的αＪＢ＝αＪπ±／（１－δ<ｍＢ>／ＭＫ，是基本強子發射源的Bose強子的倒易統計起伏。因此<（ＮＪＢ）3><ＮＢ>3＝（ＭＫ－<ｍＢ>ＭＫ－ｍπ）3［<Ｎ３π><Ｎπ>3＋3<Ｎ2π><Ｎπ>2（<ＮＫ><Ｎπ>）＋3<Ｎ2Ｋ><ＮＫ>2（<ＮＫ><Ｎπ>）2＋<Ｎ3Ｋ><ＮＫ>3（<ＮＫ><Ｎπ>）3］（19）
<Ｎ2π><Ｎπ>3＝23／β3π〖〗Γ（3／2－4γＢ）·32·Γ（3／2）·（2－4γＢ）·Γ（2－4γＢ）(20)
則
<（ＮＪＢ）3><ＮＪＢ>3≈（１－δ<ｍＢ>ＭＫ）3［3（2＋2γＢ）＋３（<ＮＫ><Ｎπ>）（1＋1απ±）］(21)
比較(13)式與(17)～(21)式得知：三階積分關聯比二階積分關聯具有更強的質量效應。為此，將作者的結果與NA22實驗數據進行以下比較：將(17)式中的αB用實驗值代替(因為(13)式與NA22實驗值相符合)，得到實驗值<Ｎ3Ｂ>／<ＮＢ>３＝2.298(1±0.14)；將(21)式代入(18)式，得到3（１＋２γＢ）（１－δ<ｍＢ>ＭＫ）3×（１＋0.06）＝2.298(1±0.014)(22)
若－２γＢ（ｇＫ）＝0.09，我們有δ<ｍＢ>／ＭＫ＝0.074±0.012。按四階積分關聯峭度(Kurtosis)的定義為γ2（ｇＲ，<ｍＢ>）＝<(ＮＢ－<ＮＢ>）4><<Ｎ2Ｂ>－<ＮＢ>2>4(23)
顯然γ2（ｇＲ，<ｍＢ>）＝α2Ｂ［<Ｎ4Ｂ><ＮＢ>4－4<Ｎ３Ｂ><ＮＢ>3＋６αＢ＋３］(24)
這裡<Ｎ3Ｂ>／<ＮＢ>3與(18)式中相同<Ｎ3Ｂ>／<ＮＢ>3＝2.298(1±0.14)(NA22實驗值)，αB的表達式(12)的質量效應與實驗精確符合，因此集中研究<Ｎ４Ｂ>／<ＮＢ>４並與NA22數據進行比較。令ＮＢ＝ＮＪＢ＋ＮＪ，ＮＪＢ為J0源的Bose強子數。再令ＮＪＢ＝Ｎπ(J0源π±介子數)，我們有<Ｎ4Ｂ><ＮＢ>4＝（１－δ<ｍＢ>ＭＫ）4［<Ｎ4π><Ｎπ>4＋4（<ＮＪ><Ｎπ>）<Ｎ3π><Ｎπ>3＋6<Ｎ２π><Ｎπ>２×（<ＮＪ><Ｎπ>）2<Ｎ2Ｊ><ＮＪ>２＋４（<Ｎ２Ｊ><Ｎπ>）3（<Ｎ3Ｊ><Ｎπ>3）＋<Ｎ4J><ＮJ>4(<ＮＪ><Ｎπ>）4］(25)
這裡，<Ｎ2π>／<Ｎπ>2＝1＋1／απ，<Ｎ2Ｊ>／<ＮＪ>2＝1＋1／αＪ，αＪ≈απ，<ＮＪ>／<Ｎπ>＝0.12(NA22數據)，<Ｎ3π>／<Ｎπ>3≈3（１＋２γＢ），得<Ｎ4π><Ｎπ>4＝24／β2π〖〗Γ（3／2－4γＢ）·Γ（3）·Γˉ7／24γＢ）(26)
其數值結果為：<Ｎ4π>／<Ｎπ>４＝15(1＋5.7γＢ）／2，可得質量效應的數值方程為（１－δ<ｍＢ>ＭＫ）4×15〖〗2（1＋5.7γＢ）＝3.246(1±0.16)(27) 由此得出： δ<ｍＢ>／ＭＫ＝0.0298±0.0025，比γ1（ｇＲ，<ｍＢ>)的(22)式所得值略小。
3、結論
關於KNO標度的爭論問題。認為多重數分布、能量、動量分布及其動力學關聯中存在量子場反常維度的效應(AD效應)，由多重數分布的NA22數據及UA5數據所確定的4γＢ（ｇＲ）＝－(0.214±0.042)，AD效應對KNO標度僅有微弱破壞。
根據短距離量子場(aqN)νKν(aqN)廣函分布對多重數分布的研究(包括上述研究結果)，目前可能得出的結論如下。
1、AD效應對q階積分關聯的影響較小，而質量效應與［（ＭＫ－ｍπ）／（ＭＫ－<ＭＢ>）］ｑ成正比。
2、KNO標度對基本強子發射源仍然成立，質量效應與AD效應破壞了KNO標度，必須扣除。
3、由半群對稱性得到的蘭道不等式成立：αB＜αmas=4，KNO標度的理論基礎是量子場論的重整化群方程，KNO標度是半群對稱性的表現。
4、短距離量子場的π±介子數Nπ的分布(14)式符合有關全部數據，特別是是NA22數據，(８)式與動量、多重數關聯中的有關性質完全相同。
5、三階積分關聯比二階積分關聯具有更強的質量效應。
由重整化群方程證明，KNO標度是嚴格的。但是，這個方程是從微擾論得到的，而它對量子場論非微擾(解析)性質，如QCD漸進自由、QED(量子電動力學)紅外穩定的研究結果已得到實驗的肯定。用半群運算元(SeimigroupOperator)與偏微分方程的數學理論來研究Ｇ（Ｎ）ａ（ｇＲ，ｍＲ，Ｐ）的對稱性，可得出非微擾重整化群方程。
相關的觀點
核子（強子）是夸克、膠子的束縛態，由量子色動力學ＱＣＤ描述。由於ＱＣＤ的基本特性（高能標度下的漸近自由、低能標度下色禁閉及動力學手征對稱性破缺），對核子（強子）結構和性質的ＱＣＤ圖象是標度相關的，在高能標度下描述強子的是與探測強子結構的硬過程相聯繫的ＱＣＤ部分子模型，強子的夸克、膠子結構信息通過ＱＣＤ部分求和規則得到，ＱＣＤ微擾論是適用的理論，在低能標度時，必須發展ＱＣＤ非微擾途徑來描述核子（強子）。
雖然夸克模型當時取得了許多成功，但也遇到了一些麻煩，如重子的夸克結構理論認為，象Ω-和Δ++這樣的重子可以由三個相同夸克組成，且都處於基態，自鏇方向相同，這種在同一能級上存在有三個全同粒子的現象是違反泡利不相容原理的。泡利不相容原理說的是兩個費米子是不能處於相同的狀態中的。
夸克的自鏇為半整數，是費米子，當然是不能違反泡利原理的。但物理學家自有辦法，你不是說三個夸克全同嗎？那我給它們來個編號或著上“顏色”（紅、
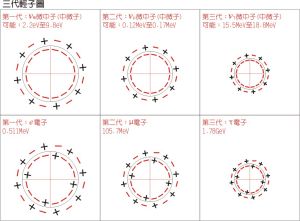三代輕子圖黃、藍），那三個夸克不就不全同了，從而不再違反泡利原理了。的確，在1964年，格林伯格引入了夸克的這一種自由度——“顏色”的概念。當然這裡的“顏色”並不是視覺感受到的顏色，它是一種新引入的自由度的代名詞，與電子帶電荷相類似，夸克帶顏色荷。這樣一來，每味夸克就有三種顏色，夸克的種類一下子由原來的6種擴展到18種，再加上它們的反粒子，那么自然界一共有36種夸克，它們和輕子（如電子、μ子、τ子及其相應的中微子）、規範粒子（如光子、三個傳遞控制夸克輕子衰變的弱相互作用的中間玻色子、八個傳遞強（色）相互作用的膠子）一起組成了大千世界。夸克具有顏色自由度的理論得到了不少實驗的支持，在70年代發展成為強相互作用的重要理論——量子色動力學。
1964年，美國物理學家默里·蓋爾曼和G.茨威格各自獨立提出了中子、質子這一類強子是由更基本的單元——Quark組成的。它們具有分數電荷，是基本電量的2/3或-1/3倍，自鏇為1/2。夸克一詞是蓋爾曼取自詹姆斯·喬埃斯的小說《芬尼根徹夜祭》的詞句“為馬克檢閱者王，三聲夸克（ThreequarksforMusterMark）”。夸克在該書中具有多種含義，其中之一是一種海鳥的叫聲。他認為，這適合他最初認為“基本粒子不基本、基本電荷非整數”的奇特想法，同時他也指出這只是一個笑話，這是對矯飾的科學語言的反抗。另外，也可能是出於他對鳥類的喜愛。
