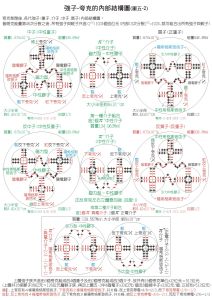
意義
板田模型不僅能把當時所知道的強子都由質子、中子和超子這三個基礎粒子複合出來,而且使比較抽象的奇異數變得具體化了,即每個強子的奇異數正好就是它所包含的反超子數和超子數之差。此外,它還預言了η°粒子的存在並為以後的實驗所證實。
但是這畢竟是比較粗糙的模型。如從量子數的角度出發,可以認為π介子是由一個質子與一個反中子複合而成的。可是從質量的角度來看,就有難以解釋的困難。因為一個核子與一個反核子,總的靜止質量約為1880兆電子伏,而一個π介子的靜止質量約為140兆電子伏,兩者相差十幾倍。兩個較重的基礎粒子,如何“複合”成一個輕得多的複合粒子呢?另外,對於後來發現的Ω-粒子,這個模型也無法解釋。儘管如此,坂田模型畢竟是將物質具有無限層次這一思想具體化的一次可貴的嘗試,它為基本粒子模型的研究開闢了道路,對於揭示強子的內部結構,推動粒子物理學的發展具有重要意義。
模型
名稱
符號
質量(MeV)
壽命(s)
IG(Jr)C
光子
y
<3×10-33
∞
0,1(1-)-
輕子
電子
e
0.511
>1022年
電子
中鐵子
ve
<46cV
穩定
μ子
μ
105.659
2.197×10-6
μ中微子
vμ
<0.25
穩定
介子
π子
π±
139.568
2.603×10-8
1-(0-)
π0
134.964
0.87×10-16
1-(0-)+
η子
η
548.8
г=1.05KeV
0+(0-)+
K子
K±
493.667
1.237×10-8
K0
497.72
K!:0.8923×10-10
K!:5.183×10-8
質子
質子
p
938.279
>1031—32年
中子
n
939.573
898±16
A子
A
1115.60
2.632×10-10
∑子
∑+
1189.37
0.800×10-10
∑0
1192.46
5.6×10-20
∑-
1197.34
1.482×10-10
Ω-子
Ω-
1672.45
0.322×10-10