SU(3)對稱性
正文
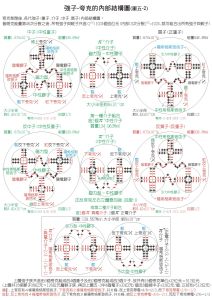強子-內部結構模型圖歷史 隨著科學技術的進步，人們製造和探測高能粒子的手段不斷更新，發現的新粒子、新現象越來越豐富。20世紀50年代確立了一系列奇異粒子，60年代又陸續發現了為數眾多的共振態粒子，使得當時已發現的粒子（主要是強子）的數目猛增至一二百個之多，大大超出了發現元素周期律時已發現的化學元素的數目。在這種情況下，把這么許多粒子進行科學的分類，找出它們性質之間的內在聯繫，並進而追溯這些聯繫的根源，就成了當時十分迫切的課題。
在這樣的基礎上，60年代前期，經過許多科學工作者的共同努力，包括大量深入的理論探索和細緻周密的實驗分析，揭示了強子的SU(3)對稱性，利用SU(3)群把同位鏇對稱性和超荷對稱性結合起來，統一到一個更大更高的內部對稱群中去，發展並最後確立了關於強相互作用粒子的SU(3)對稱性理論。
強子SU(3)對稱性的建立 利用SU(3)群來研究強子對稱性的早期嘗試,與強子結構的坂田模型密切相關。50年代初，高能物理中發現了一系列奇異粒子，引入了奇異數，並總結出了著名的蓋耳－曼－西島法則。在此基礎上日本物理學家坂田昌一在1955年提出了坂田模型，假定所有的強子都是由質子(p)、中子(n)和Λ 超子以及它們的反粒子組成的。正像忽略去質子和中子的差別以後核力和核子體系具有同位鏇對稱性【即 SU(2)對稱性】一樣，如果人們忽略Λ 粒子與核子之間的差異，而把它們看作同一粒子所處的三種不同狀態，它們之間應具有SU(3)對稱性，由它們所構成的強子體系也應具有SU(3)對稱性。
強子-內部結構表 D(0,0)＝1，D(1,0)＝3，D(0,1)＝3*，D(1,1)＝8，
其中3*是3的共軛表示。
在SU(3)變換下,基本的(p，n，Λ)具有重子數N＝1，按基礎表示3變換,相應的反粒子(圴，嬞，揈)具有重子數N＝-1，按共軛表示3*變換。按坂田模型,N＝0的介子由一對正反(p，n，Λ)組成，它們應按表示8和1變換。當時實驗上已確認的贗標介子只有同位鏇三重態的普通介子(π- ,π0 ,π+ )和兩個同位鏇雙重態的奇異介子(K0 ，K+ 和K- ,噖0 ),它們一共有七個。根據SU(3)對稱性預言至少應當存在一個同位鏇單態的普通介子，與上述七個粒子組成SU(3)八重態。不久果然在實驗上發現了單態非奇異介子η(548)。與贗標介子的情形相似，先後在實驗上發現的矢量介子ρ(ρ- ，ρ0 ，ρ+ )、K* (K*0 , K*+ ；K*- ,噖*0 )、ω和嗞一共九個,適合於填充可約表示8)+1。可見,以坂田模型為基礎的SU(3)對稱方案很好地解釋了介子的性質。
但是，坂田模型關於重子的分類方案卻遇到了原則性的困難。例如，重子數N＝1超荷Y＝0的Σ超子三重態可能填充的不可約表示是6*或15。但6*中根本沒有另一個超子(Y=-1的雙重態)Ξ的位置；而15中雖然可以容納Ξ超子，卻還預言許多至今都沒有任何跡象的空額粒子。
1961年在重新仔細分析實驗資料的基礎上,M.蓋耳－曼和Y.奈曼提出了新的八重態分類方案（稱為八重法），假定八個重子（N,Ξ,Σ和Λ）和八個贗標介子(K,噖,π和η)一樣,屬於不可約表示8。按照SU(3)群表示的乘法規則，主要衰變為一對贗標介子的矢量介子共振態和主要衰變為一個贗標介子和一個
重子的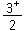
重子共振態都應當屬於不可約表示27,10,10*,8或1。 根據實驗分析,同坂田模型中一樣,九個矢量介子填充可約表示8+1。自鏇宇稱為
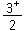的重子起初共發現九個，這就是非奇異的四重態Δ(1232)(Δ- ，Δ0 ，Δ+ ,Δ++ )，超荷Y=0的三重態
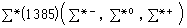和Y＝-1的雙重態Ξ*(1530)
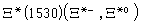。在SU(3)群八重法分類方案中自然地把它們歸入不可約表示10，但其中還要求存在一個新的Y=-2的同位鏇單態穩定重子Ω- 。根據表示中其他粒子的質量，理論預言Ω- 的質量約為1675MeV。1964年，N.P.薩穆斯在實驗上果然發現了這個粒子。以後,實驗還測定了它的質量為1672.45±0.32MeV,自鏇宇稱為3+ /2，它的主要弱衰變方式
和壽命 (0.819±0.027)×10-10 s，這些都與理論預言相符合。這是對SU(3)對稱性八重態分類方案的強有力支持。 SU(3)對稱性的主要結果 有以下幾點。
①粒子填充和分類。現已確認的常見介子和重子在SU(3)對稱性中按下述方式分類。
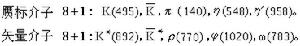
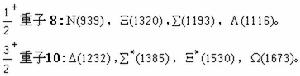
粒子符號後括弧中的數字是指該同位鏇多重態質量平均值,以MeV為單位。每一組稱為一個 SU(3)多重態。非單態粒子的填充情況可以用下圖表示。
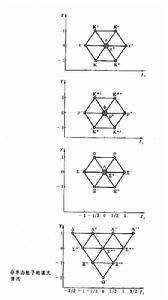SU(3)對稱性
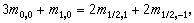（1a）
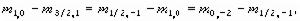（1b）
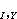是同位鏇-超荷量子數為(I，Y)的狀態的質量。實驗上,對重子，式(la)兩邊的觀察值的四分之一分別為1135MeV和1128MeV,故此式在0.6％的精度範圍內成立。對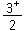重子,式(lb)中三個質量差分別是152、149和139MeV。 對於介子八重態，通常認為套用質量二次方代替式(la)中的質量，加上電荷共軛性質的考慮，可得
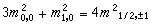(1c)
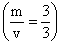
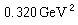，而mn=0.301GeV2 ，相差約6％，說明η介子與後來發現的第九個贗標介子 η′(958)有某些混合。對於矢量介子九重態,相應的兩個(I，Y)=(0，0)的狀態有較大的混合，有很多專門的討論。 ③磁矩關係。電荷算符在 SU(3)變換下的性質由蓋耳－曼－西島法則確定，由此可導得一個多重態內諸粒子磁矩的相互關係。例如：
(2)
2.793=2.379±0.020，
-1.1±0.05=-1.85±0.75，
-1.250±0.014=-1.913，
量級上是符合的。
④電磁質量差。由電荷算符的性質還可以導出一個同位鏇多重態內不同電荷粒子質量的"超精細"分裂。對
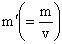重子，可得到關係式： 
(3)
⑤強衰變寬度。按照SU(3)對稱性，同一個SU(3)多重態內各個粒子看成同一粒子的不同內部態，因此各個粒子的相應衰變方式的幾率之間就存在著一定的關係。
60年代前期,圍繞著SU(3)對稱性的理論預言和實驗檢驗做了大量的工作。討論了其他各種粒子的分類填充方案和質量關係，分析了強子的各種（包括強的和電磁的）衰變方式和衰變寬度，以及各種散射截面之間的關係，研究了強子的弱相互作用性質和選擇規則等等。SU(3) 對稱性理論的一系列推斷和預言都同實驗有較好的符合。大體說來，和粒子的靜止性質（內部性質）相聯繫的那些理論預言同實驗結果符合得較好一些，而對於那些同粒子的運動性質（外部性質）關係較密切的過程，情況要複雜一些，理論與實驗的符合程度要差一些。
SU(3)對稱性理論提供了一個可靠而有力的工具,對長期積累起來的豐富的實驗資料作出了系統的分析，對數以百計的強子進行了貼切的分類，較成功地對這些粒子的基本屬性（包括質量譜的規律性）作出了解釋。從這個意義上說,強相互作用粒子的SU(3)對稱性同化學元素的周期律十分相似。
SU(3)對稱性和強子結構 關於強相互作用粒子,從一開始 SU(3)對稱性的研究就是同強子結構的坂田模型緊密相關的。受到實驗廣泛支持的八重法正是從坂田模型中脫胎出來而又經過原則性的改造而得到的。另一方面，八重態有一個十分顯著的特點：所有介子都僅僅填充1、8表示，這兩個表示可以由基礎表示3和3*的乘積組成，所有重子都僅僅填充8、10表示，它們可以由三個3表示的乘積組成,這一點啟發蓋耳-曼和G.茲韋克提出如下的假定：存在著具有分數重子數、分數電荷和分數超荷量子數的三種基礎粒子(u，d,s)，稱為夸克，它們按SU(3)群的基礎表示3變換；一切強子都是由夸克及其反粒子組成的。介子由一對正反夸克組成，應屬於表示8和1,重子由三個夸克組成,應屬於表示10、8和1。強子之間的SU(3)對稱性正是由夸克的基本SU(3)屬性所決定的。這就是夸克模型。夸克模型成功地解釋了強子的SU(3)對稱性，並且導出了一系列新的結果,得到了實驗的廣泛支持。
由此可見，正像化學元素周期律反映了各種元素原子中電子排布的規律性,揭示了原子的內部結構一樣,強相互作用的 SU(3)對稱性深刻地反映了強子的內部結構特徵。
