峭度

峭度的定義

峭度（Kurtosis）K是反映振動信號分布特性的數值統計量，是歸一化的4階中心矩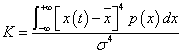

	式中：x(t)為瞬時振幅；x槓為振幅均值；p(x)為機率密度；σ為標準差。

　離散化的公式：

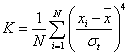	式中：xi為信號值，xi槓為信號均值；N為採樣長度；σt為標準差。

峭度的意義

峭度係數的意義如圖1所示。當K=3定義為分布曲線具有正常峰度（即零峭度）；當K>3時，分布曲線具有正峭度。由(式2)可知，當標準差σt小於正常狀態下的標準差，即觀測值的分散程度較小時，K增大，此時常態分配曲線峰頂的高度高於正常常態分配曲線，故稱為正峭度。當K<3時，分布曲線具有負峭度，由(式2)可以看出，當標準差σt大於正常狀態下的標準差，即觀測值的分散程度較大時，K減小，此時常態分配曲線峰頂的高度低於正常常態分配曲線，故稱為負峭度。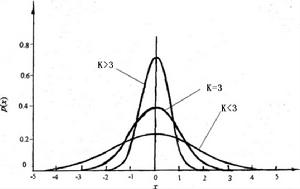

峭度的套用

峭度指標是無量綱參數，由於它與軸承轉速、尺寸、載荷等無關，對衝擊信號特別敏感，特別適用於表面損傷類故障、尤其是早期故障的診斷。
在軸承無故障運轉時，由於各種不確定因素的影響，振動信號的幅值分布接近常態分配，峭度指標值K≈3;隨著故障的出現和發展，振動信號中大幅值的機率密度增加，信號幅值的分布偏離常態分配，正態曲線出現偏斜或分散，峭度值也隨之增大。峭度指標的絕對值越大，說明軸承偏離其正常狀態，故障越嚴重，如當其K>8時，則很可能出現了較大的故障。