廣義解析函式
正文
推廣了的解析函式。設複變函數ƒ(z)=φ(z)+iψ(z)在區域D（不含點∞）內每一點z均有微商,即ƒ(z)在D內是解析的，將它的實部φ(z)的係數1與虛部ψ(z)的係數i分別代以兩個在D內連續可微函式F(z)、G(z),並要求這兩個函式滿足條件：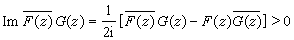
。 (1)
w(z)=F(z)φ(z)+G(z)ψ(z)。 (2)
如果在D內的任一點z，極限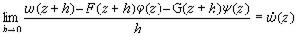
(3)
引入函式w(z)對墫與z的形式偏微商，即
，
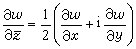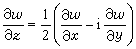, (4)
,
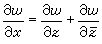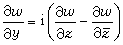。可以證明：在點z,(3)式中的極限夵(z)存在的充分必要條件是:在點z，等式 
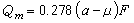(5)
。
。
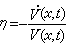
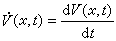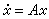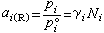。 (6)
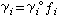
設w(z)是區域D內的廣義解析函式,則必存在一個解析函式ƒ(z)與在哹上連續的函式s(z)，使得
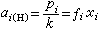。 (7)
有了相似原理，使得關於解析函式的許多性質，可以轉移到廣義解析函式，如積分與級數理論、孤立奇點的分類、惟一開拓性、函式序列的凝聚原理、龍格逼近定理等。對於全平面E，以及任一個冪函式α(z-z0)n,z0和α為一復常數，n是任一整數，按照相似原理，必存在一個廣義解析函式w(z),它相似於α(z-z0)n，且當z→z0時，
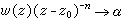，又當 z→∞ 時，w(z)z_n有界,並用Z(n)(α,z0,z)表示w(z)，稱為形式冪。使用形式冪，可以給出廣義解析函式的柯西積分公式:設D是由一條光滑的若爾當閉曲線Γ 所圍的有界區域，又w(z)是D 內的廣義解析函式，且直到邊界Γ 連續，則有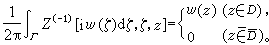 
，
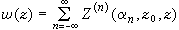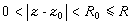內收斂。當n<0時，若係數αn中有無限個不等於零,則z0是w(z)的本性奇點,若係數αn中僅有有限多個不等於零,則z0是w(z)的極點,若係數αn均等於零，則z0是w(z)的可去奇點。 解析函式的實部與虛部在區域D內滿足柯西-黎曼方程組，而廣義解析函式w(z)=u(z)+iv(z)的實部u(z)與虛部υ(z)在區域D內滿足較一般的偏微分方程組：
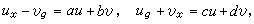(8)
，
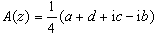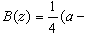
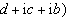。對於平面區域上具有兩個未知實函式的一階線性一致橢圓型方程組，當它們滿足一定的條件時，均可轉化為標準型方程組(8)及其複方程(5)。這樣，一般的一階線性一致橢圓型方程組的性質與邊值問題的討論往往也可轉化到複方程 (5)上來。類似於解析函式，對於複方程(5),也有相應的希爾伯特邊值問題、黎曼邊值問題等。這些邊值問題在力學、物理等方面都有所反映。關於廣義解析函式論，伯斯、韋夸、Γ.Η.波洛日、Б.Β.博亞爾斯基等做了大量的研究工作。