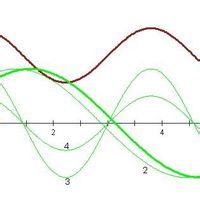
定義
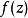 本性奇點
本性奇點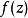 本性奇點
本性奇點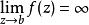 本性奇點
本性奇點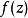 本性奇點
本性奇點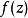 本性奇點
本性奇點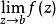 本性奇點
本性奇點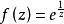 本性奇點
本性奇點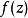 本性奇點
本性奇點如果函式 在其孤立奇點b的一個去心鄰域內展開成洛朗級數,其中含有無窮多個(z-b)的負冪項,則稱b點為 的本性奇點。這與前面的定義是一致的,因為如果 時函式 在b點鄰域內展成的洛朗級數含有有限個(z-b)的負冪次項,那么,若 在b點的洛朗展開式含有無窮多個(z-b)的負冪次項,則極限 必然不存在,而這正是前面給出的本性奇點定義。例如,函式 ,當z=0時其值不確定,而在z=0的鄰域內解析,所以z=0是 的孤立奇點。它展開成冪級數為
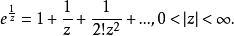 本性奇點
本性奇點含有無限多個負冪項,所以z=0是它的本性奇點。
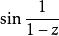 本性奇點
本性奇點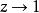 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點又如,z=1是函式 的孤立奇點,當 時,該函式的極限不存在,且不為 ,所以z=1是該函式的本性奇點。也可以在 環域內將該函式展開成洛朗級數
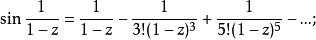 本性奇點
本性奇點可見,上式有無窮多個(1一z)的負冪項。所以z=1是該函式的本性奇點。
本性奇點的特性
 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點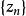 本性奇點
本性奇點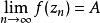 本性奇點
本性奇點定理1(維爾斯特拉斯定理) :設 為函式 的孤立奇點,則 為 的本性奇點的充分必要條件是:對於任何複數A(包括無窮),一定存在收斂於 的序列 ,使得 .
 本性奇點
本性奇點換句話說,在本性奇點的無論怎樣小的鄰環內, 可以任意接近預先給定的任何有限數或趨於無窮.
證 : 由本性奇點定義可知,條件的充分性是明顯的,以下證明必要性.
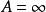 本性奇點
本性奇點 本性奇點
本性奇點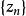 本性奇點
本性奇點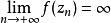 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點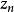 本性奇點
本性奇點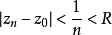 本性奇點
本性奇點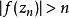 本性奇點
本性奇點 本性奇點
本性奇點(1)若 ,我們要證明存在一個收斂於 的序列 ,使得 .事實上,因為 是 的本性奇點,所以 在 的鄰環內無界。也就是說,對於任意正整數n,都可以找到點 滿足 ,使得 .於是,有一個趨於 的序列{%),使
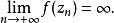 本性奇點
本性奇點 本性奇點
本性奇點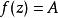 本性奇點
本性奇點 本性奇點
本性奇點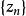 本性奇點
本性奇點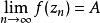 本性奇點
本性奇點 本性奇點
本性奇點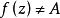 本性奇點
本性奇點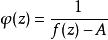 本性奇點
本性奇點 本性奇點
本性奇點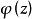 本性奇點
本性奇點 本性奇點
本性奇點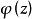 本性奇點
本性奇點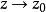 本性奇點
本性奇點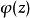 本性奇點
本性奇點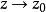 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點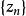 本性奇點
本性奇點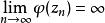 本性奇點
本性奇點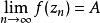 本性奇點
本性奇點(2)若A是任意有限複數.如果在 點的任意小的鄰環內均存在z點,使得 ,則顯然有一個趨於 的序列 ,使 .如果存在 的一個鄰環,在其中.則函式在這個鄰環內解析,並且可以證明是的本性奇點.事實上,如果是的可去奇點或極點,則當時趨於有限數或無窮大.從而,當時趨於有限數,與為的本性奇點的假設矛盾.於是,根據(1)的證明,必存在趨於的序列,使得.因此,.定理證畢。
 本性奇點
本性奇點 本性奇點
本性奇點 本性奇點
本性奇點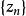 本性奇點
本性奇點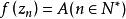 本性奇點
本性奇點定理2(畢卡定理) : 如果為的本性奇點,則對於每一個有限複數 A(至多有一個例外值),均有趨於的點列,使。