例子
例如函式：
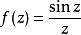可去奇點對z≠ 0 有一個奇點z= 0。藉由定義f(0)=1，可將此奇點消去，並得到全純的sinc函式。
確切地，如果U是複平面C的一個開集，a是U中一點，f:U- {a} →C是一個全純函式，如果存在一個在U- {a} 與f相等的全純函式g:U→C，則a稱為f的一個可去奇點。如果這樣的g存在，我們說f在a是可全純延拓的。
黎曼定理
黎曼關於可去奇點的定理指出了何時一個奇點是可去的：
定理下列情形是等價的：
i)f可全純延拓到a。
ii)f可連續延拓到a。
iii) 存在a的一個鄰域，在它上面f有界。
iv) limz→a(z - a)f(z) = 0.
蘊含關係 i) ⇒ ii) ⇒ iii) ⇒ iv) 是平凡的。為了證明 iv) ⇒ i)，我們首先回憶到一個函式在a的全純性等價於解析，即有一個冪級數表示。定義
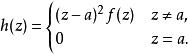可去奇點則
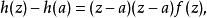可去奇點這裡由假設(z - a)f(z)可以視為一個D上的連續函式。換句話說，h在D上全純從而有在a的泰勒級數：
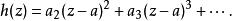可去奇點所以
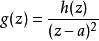可去奇點是f在a的全純延拓，這就證明了先前的斷言。
其它類型奇點
不像實變數函式， 全純函式有足夠的剛性使得其孤立奇點可完全分類。一個全純函式的奇點要么其實不是真正的奇點，即可去奇點，要么是如下兩類居其一：
受黎曼定理啟示，給定一個不可去奇點，我們可能問是否存在一個自然數m使得 limz→a(z - a)f(z) = 0。如果存在，a稱為f的一個極點，這樣最小的m稱為a的階數。所以可去奇點恰好是零階極點。一個全純函式在極點附近一致發散到無窮遠點。
如果f的一個孤立奇點a既非可去奇點也非極點，則稱本性奇點。皮卡定理指出f將任意穿孔開鄰域U- {a} 映滿整個複平面，至多少一個可能的例外點。
1.受黎曼定理啟示，給定一個不可去奇點，我們可能問是否存在一個自然數m使得 limz→a(z - a)f(z) = 0。如果存在，a稱為f的一個極點，這樣最小的m稱為a的階數。所以可去奇點恰好是零階極點。一個全純函式在極點附近一致發散到無窮遠點。
2.如果f的一個孤立奇點a既非可去奇點也非極點，則稱本性奇點。皮卡定理指出f將任意穿孔開鄰域U- {a} 映滿整個複平面，至多少一個可能的例外點。
參見
•解析容量（Analytic capacity）
•可去不連續點（Removable discontinuity）
