解析函式邊值問題

解析函式邊值問題是指尋求滿足一定邊界條件的解析函式的一類問題，是解析函式論在許多理論和實際問題中套用極為廣泛的一個重要分支。

解析函式邊值問題

正文

尋求滿足一定邊界條件的解析函式的一類問題，這是解析函式論在許多理論和實際問題中套用極為廣泛的一個重要分支。下面是兩個最典型的例子。
黎曼邊值問題 設l為複平面上一組有向的光滑曲線，把平面分割為若干個連通區域,要求一分區全純函式(即在上述每一個連通區域內全純）φ(z)使

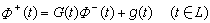， 　 (1)

式中G(t),g(t)都是已知函式，而φ +(t)和φ -(t)分別表示當z從l的正側（即沿l正向前進時的左側）和負側(右側)趨於l上一點時φ(z)的極限值亦即邊值。此外還應補充要求φ(z)在無窮遠處至多有一極點。如果l中含有開口弧段，則也應說明要求φ(z)在l的端點附近的性態:具有不到一階的奇異性。在G(t),g(t)滿足一定的條件時,這一問題已完全解決。
希爾伯特邊值問題　設G為一區域，l為其邊界，取其正向使G在其左側，要求在G內的一全純函式φ(z)，使

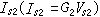(2)

式中α(t)，b(t),с(t)都是l上已給的實函式。特別,當α(t)=1,b(t)=0時，則此希爾伯特邊值問題就是解析函式的狄利克雷問題。當α(t),b(t),с(t)滿足一定的條件時，上述邊值問題已有較完整的討論,但對G為多連通區域的情況還不能說已完全徹底解決。
有人把黎曼邊值問題稱作希爾伯特邊值問題，而把希爾伯特邊值問題稱作黎曼－希爾伯特邊值問題。這兩個問題是有密切聯繫的，求解它們的主要工具都是柯西型積分。
進一步推廣是在(1)或(2)中可以含有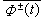或者含有φ +(α(t)),φ -(α(t))，其中α(t)為l映於自身的一個同胚映射，保向或逆向，稱為l的位移。這樣,相應的問題就稱為帶共軛的或帶位移的邊值問題，當然也有既帶共軛又帶位移的邊值問題。
如果把(1)或(2)中的φ(z)看作N維分區全純向量，而把G(t),α(t),b(t)看作N×N矩陣,g(t),с(t)也看作N維向量,則就構成了分區全純向量的邊值問題。這類問題雖也有許多工作，但與N=1的情況相比較,還遠遠沒有達到完善的地步。
由於解析函式概念可推廣為廣義解析函式（基於把解析函式的實部、虛部所滿足的柯西－黎曼方程組推廣為較一般的一階偏微分方程組），因此解析函式邊值問題也可推廣為廣義解析函式邊值問題，這是把函式論與偏微分方程結合起來的一個方向。
解析函式邊值問題和廣義解析函式邊值問題在奇異積分方程方面有廣泛的套用，它們在彈性力學、流體力學方面也有重要的套用。這些方面的理論及其套用，主要是由蘇聯學者建立和發展起來的。自20世紀60年代以來，中國的數學工作者在這些方面也做了不少工作。

配圖

相關連線