英文名稱
因式定理
Factor theorem
因式定理釋義
x-a is a factor of a polynomial P(x) with integral coefficients if and only if P(a)=0
定義
因式定理：
“設f(x)為一多項式，則x-a為f(x)的因式”等價於f(a)=0。
推廣：
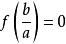因式定理“ax-b為f(x)的因式”等價於。
餘式定理：當一個多項式f(x) 除以(x – a) 時， 所得的餘數等於 f(a) 。
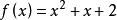因式定理
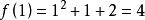因式定理例1：當除以 (x – 1) 時，則餘數等於。
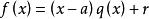因式定理整係數多項式f(x)除以(x-a)商為q(x)，餘式為r，則。
如果多項式r=0，那么多項式f(x)必定含有因式(x-a)。反過來，如果f(x)含有因式(x-a)，那么，r=0。
餘式定理的推論
當一個多項式 f(x) 除以 (mx – n) 時，所得的餘數等於 f(n/m) 。
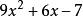因式定理例2：求當 除以 (3x + 1) 時所得的餘數。
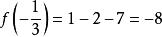因式定理設 f(x) = 9x^2 + 6x – 7，則餘數。
例題
圖1如圖1，此題可以利用完全立方公式解答，但較為繁瑣。
仔細觀察不難發現，當x=y時，原式的值為0。
根據因式定理可知：原式必有因式x-y。
同樣的，可以得到原式必有因式y-z和z-x（也可以由原式為對稱多項式直接得到）；
然後再用待定係數法（結合賦值法）求出待定係數即可。
意義
熟練掌握因式定理後，可以運用試根法（結合因式定理）找到因式，再用待定係數法（結合賦值法）求出待定係數，或綜合除法直接求出剩下的因式，這樣就可以較便利的分解因式了。
同時，將因式定理與待定係數法配合使用往往可以更簡便的進行因式分解，也可以用來判斷能否進行因式分解。
多項式的因式分解
因式定理普遍套用於找到一個多項式的因式或多項式方程的根的兩類問題。從定理的推論結果，這些問題基本上是等價的。
若多項式已知一個或數個零點，因式定理也可以移除多項式中已知零點的部份，變成一個階數較低的多項式，其零點即為原多項式中剩下的零點，以簡化多項式求根的過程 。方法如下：
1、先設法找出多項式的一個零點；
2、利用因式定理確認是多項式的因式；
3、利用長除法計算多項式；
4、多項式方程中所有滿足條件的根都是方程式的根。因為多項式階數較小，因此要找出多項式的零點可能會比較簡單。
另外欲使A=BQ+R成立，就令除式BQ=0,則被除式A=R，能使此方程式成立，即
1、被除式=(商式)(除式)+餘式
或是
2、被除式/除式=商式+餘式/除式
