定理定義
閉區間套
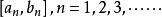閉區間套定理設有無窮多個閉區間，滿足以下兩個條件：
(1)[a,b]⊂[a,b]（即後一個閉區間都在前一個閉區間之內）；
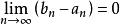閉區間套定理(2)（即只要n充分大，閉區間的長度與0就可以接近到預先給定的程度），
閉區間套定理那么將這一無窮多個閉區間所構成的集合稱為一個閉區間套，簡稱區間套。
定理
閉區間套定理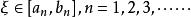
閉區間套定理
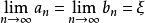閉區間套定理若是一個閉區間套，則存在唯一實數，並且。
推論
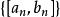閉區間套定理
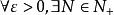閉區間套定理
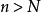閉區間套定理若ξ是閉區間套的公共點，則，當時，有[a,b]⊂U(ξ,ε)。
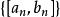閉區間套定理 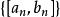閉區間套定理即如果ξ是閉區間套的公共點，那么在ξ的ε鄰域內，總有區間套的無數個區間。
推導過程
該定理反應了實數的完備性，是關於實數連續性的6個等價命題之一，因此可以由其他5個定理推導出來。但既然是關於實數連續性的定理，自然可以用實數的定義以及實數公理——戴德金定理來證明。
由閉區間套的定義，不難得到以下不等式：
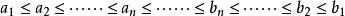閉區間套定理取所有小於b的實數構成數集A，其他實數構成集合B，則：
①{a}⊂A，{b}⊂B，因此A、B非空；
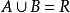閉區間套定理② ；
③明顯，A中的任意元素都小於B中的任意元素。
由戴德金定理得，存在唯一實數ξ，使ξ為A、B的分界點，並且ξ要么是A中的最大值，要么是B中的最小值。
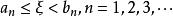閉區間套定理
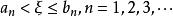閉區間套定理
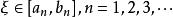閉區間套定理假設ξ是A中的最大值，則有 ；假設ξ是B中的最小值，則有 。無論哪種情況都有 。
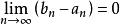閉區間套定理∵
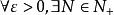閉區間套定理 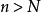閉區間套定理
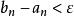閉區間套定理∴ ，當 時，
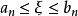閉區間套定理∵
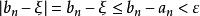閉區間套定理
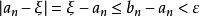閉區間套定理∴ ，
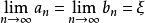閉區間套定理∴
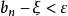閉區間套定理
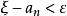閉區間套定理
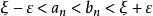閉區間套定理而 ， ，即
∴有[a,b]⊂U(ξ,ε)。
定律影響
閉區間套定理由於具有較好的構造性，因此在實數相關的命題中有廣泛的套用，故閉區間套定理不僅有重要的理論價值，而且具有很好的套用價值。例如用來證明單調有界定理，閉區間上的連續函式的性質（有界性、最值性、零點存在性、一致連續性等），拉格朗日中值定理等微分學上常用的定理。作為介紹，在這裡給出用閉區間套定理證明單調有界定理和拉格朗日中值定理的過程。
單調有界定理
單調遞增有上界，或單調遞減有下界的數列必定收斂。
證明：以單調遞增有上界的數列為例。設數列{x}單調遞增有上界b，如果數列從某一項開始，所有的項都等於某個常數a，那么a就是{x}的極限。如果不是這樣，即{x}嚴格單調，現構造一個閉區間套：
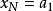閉區間套定理
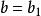閉區間套定理
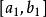閉區間套定理在{x}中任取一項 ， ，由{x}的單調性和有界性可知，下標大於N的所有x都落在 上。
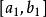閉區間套定理
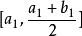閉區間套定理
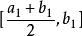閉區間套定理
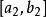閉區間套定理將 二等分成 和 ，二者之一必有{x}中的無限項，設它為 。
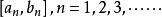閉區間套定理 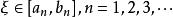閉區間套定理重複上述步驟，得到一個閉區間套 ，由閉區間套定理，存在唯一實數
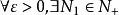閉區間套定理
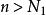閉區間套定理 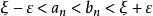閉區間套定理由閉區間套定理的推論，對 ，當 時，有。
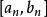閉區間套定理
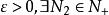閉區間套定理
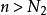閉區間套定理 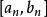閉區間套定理
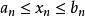閉區間套定理而根據區間套的構造，每一個 上都有{x}的無限項，利用{x}的單調性可知，對上述的 ，當時，所有的x都落在閉區間上，即。
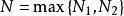閉區間套定理 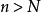閉區間套定理
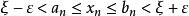閉區間套定理
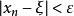閉區間套定理於是取，當時，上述不等式均成立，即有。這也就是。
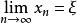閉區間套定理∴
拉格朗日中值定理
閉區間套定理
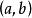閉區間套定理 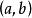閉區間套定理
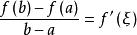閉區間套定理設f(x)在閉區間上連續，開區間上可導，則在至少存在一點ξ，使。
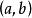閉區間套定理 閉區間套定理 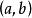閉區間套定理幾何意義是，若f(x)在上連續，上可導，則在上至少存在一點ξ，使得f(x)在該點的切線與兩端點之間的連線平行。
閉區間套定理
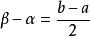閉區間套定理
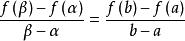閉區間套定理先介紹一個引理：若f(x)在上連續，則至少存在一個閉區間[α,β]⊂[a,b]，其中，並且滿足。
閉區間套定理 閉區間套定理這個引理在此不證，但其幾何意義十分明顯：若f(x)在上連續，連線兩端點得到一條直線l，則總能將l平移使得l與f(x)的交點之中，至少存在兩個交點橫坐標的距離為閉區間長度的一半。
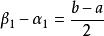閉區間套定理
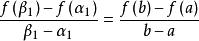閉區間套定理證明：運用上述引理，存在至少一個閉區間[α,β]⊂[a,b]，，且。
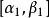閉區間套定理
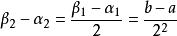閉區間套定理
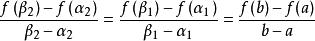閉區間套定理再對使用上述引理，得到至少存在一個閉區間[α,β2]⊂[α,β]，，且。
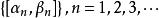閉區間套定理
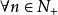閉區間套定理反覆運用上述引理，則得到一個集合，滿足閉區間套的定義，且，有
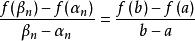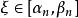閉區間套定理
閉區間套定理
閉區間套定理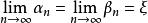
閉區間套定理由閉區間套定理，存在唯一實數，即，且。
由於f(x)在ξ處可導，按導數的定義以及海涅定理，
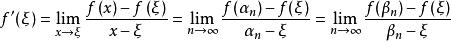閉區間套定理又由極限與無窮小的關係可知成立以下等式：
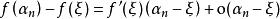閉區間套定理
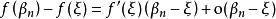閉區間套定理
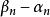閉區間套定理兩式相減，並除以，得
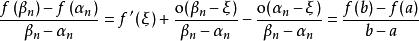閉區間套定理
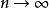閉區間套定理
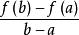閉區間套定理令，上式最右端的極限仍然是，中間式子的極限值計算如下：
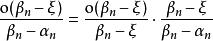閉區間套定理
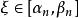閉區間套定理 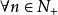閉區間套定理
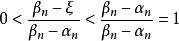閉區間套定理第一個因式是無窮小量，而因為，所以，都有，即第二個因式是有界量。根據有界函式乘以無窮小仍然是無窮小可知，中間式子的第二項是無窮小量。
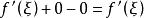閉區間套定理同理可證中間式子的第三項也是無窮小量，從而中間式子的極限值就是。
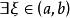閉區間套定理 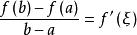閉區間套定理於是，使，拉格朗日中值定理得證。
