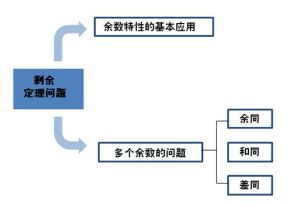
簡介
當多項式f(x)除以一線性多項式(x-a)時,所得的餘式是f(a)。如果餘式為0,x-a即f(x)的一個因式。這結果可以幫助我們把多項式作因式分解。證明
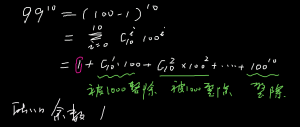 餘數定理
餘數定理設多項式P(x)除以一次式(x-a)所得的商為Q(x),餘數為R,根據上面的性質可以列出下列恆等式:
令x=a,代入上式即得P(a)=(a-a)×Q(a)+R=R。因此得到結論:P(x)除以(x-a)後的餘數R=P(a)。
注意:若除式不為(x-a)的類型,我們依然可以利用上面的方法來求餘數(式),即先求出使除式為0的x的值,再代入恆等號兩邊。參考下列例題。
例題
一次項係數不為1的場合例:求的餘數。
解:在這裡,使除式為0的x=1/2,所以餘數為。
除式次數大於1的場合
例:求的餘式。
解:由於除式是2次多項式,所以設餘式為(餘式的次數要比除式低1)。的解為x=1及x=2。代入恆等式的兩邊得:
解得。
故餘式為
例:求的餘式。
解:除式的次數為3,所以設餘式為。由於(x-1)³=0的解為x=1及x=-1,代入恆等式得:
1=a+b+c
1=a-b+c
※出現等式個數少於待定係數的個數時需要把恆等式兩邊對x求導,再把解代入求導後的等式中。
對左右兩邊求導得
再把x=1代入,得到第三個等式:10=2a+b
解方程得a=5,b=0,c=-4
所以餘式為5x²-4