定義
多項式定理是德國數學家萊布尼茲首先發現的,他將此發現寫信告訴了瑞士數學家約翰.貝努利,由貝努利完成了定理的證明。
預備知識
記號
為方便起見,定義如下記號:
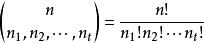 多項式定理
多項式定理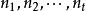 多項式定理
多項式定理 多項式定理
多項式定理其中是非負整數,滿足
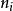 多項式定理
多項式定理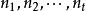 多項式定理
多項式定理意義:將 n 個元素分為 t 組,使得第 i 組有個元素的方式數,重數分別為的 t 類元素的排列數。
多項式係數的Pascal公式
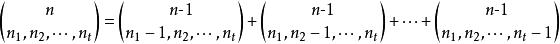 多項式定理
多項式定理定理內容
 多項式定理
多項式定理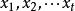 多項式定理
多項式定理設是正整數,則對 t 個實數有
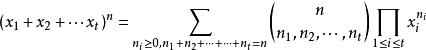 多項式定理
多項式定理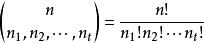 多項式定理
多項式定理其中。
定理證明
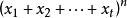 多項式定理
多項式定理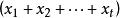 多項式定理
多項式定理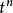 多項式定理
多項式定理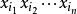 多項式定理
多項式定理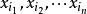 多項式定理
多項式定理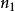 多項式定理
多項式定理 多項式定理
多項式定理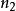 多項式定理
多項式定理 多項式定理
多項式定理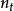 多項式定理
多項式定理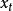 多項式定理
多項式定理 多項式定理
多項式定理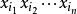 多項式定理
多項式定理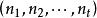 多項式定理
多項式定理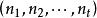 多項式定理
多項式定理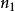 多項式定理
多項式定理 多項式定理
多項式定理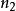 多項式定理
多項式定理 多項式定理
多項式定理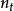 多項式定理
多項式定理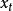 多項式定理
多項式定理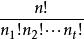 多項式定理
多項式定理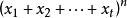 多項式定理
多項式定理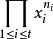 多項式定理
多項式定理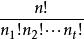 多項式定理
多項式定理是 n 個因式的乘積,其展開式中共有項,我們可以按如下方法將這些項進行分類,設是展開式中任一項,如果在中有個,個,...,個(其中有),則把歸於 類。顯然,屬於類的項的個數等於由個,個,...,個作成的全排列數,為。因此,在的展開式中(合併同類項之後),的係數為,至此該定理得證。
特殊情況
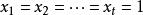 多項式定理
多項式定理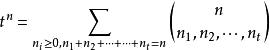 多項式定理
多項式定理(1)若取,則有:。
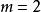 多項式定理
多項式定理(2)多項式定理是對二項式定理的推廣,在多項式定理中令就得到了二項式定理 。
推論
推論1
(二項式定理)
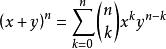 多項式定理
多項式定理設 n 為正整數,x 和 y 是任意實數,則有: 。
推論2
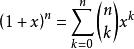 多項式定理
多項式定理設 n 為正整數,x是任意實數,則有:。
推論3
設 n 為正整數,則有:
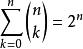 多項式定理
多項式定理(1)(令推論2中 x=1 ,則可得)。
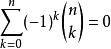 多項式定理
多項式定理(2)(令推論2中 x=-1 ,則可得)。
推論4
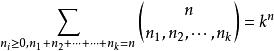 多項式定理
多項式定理 多項式定理
多項式定理(令多項式定理中的,則可得到)。

