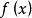定義
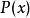 餘式定理
餘式定理 餘式定理
餘式定理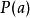 餘式定理
餘式定理餘式定理是指一個多項式 除以一線性多項式 的餘式是 }。
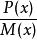 餘式定理
餘式定理 餘式定理
餘式定理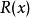 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理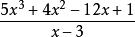 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理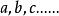 餘式定理
餘式定理我們可以一般化 餘數定理。如果 的商式是 、餘式是 ,那么 。其中 的次數會小於 的次數。例如, 的餘式是 。又可以說是把除式的零點代入被除式所得的值是餘式。 至於除式為2次以上時,可將n次除式的 根 列出聯立方程:
 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理其中 是被除式 是餘式。 此方法只可用在除式不是任一多項式的 次方。
推導
 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理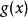 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理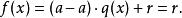 餘式定理
餘式定理餘式定理可由多項式除法的定義導出。根據多項式除法的定義,設被除式為
,除式為,商式為,餘式為,則有如果是一次式,則的次數小於1,因此,只能為常數,這時,餘式也叫餘數,記為,即有根據上式,當時,有
 餘式定理
餘式定理 餘式定理
餘式定理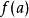 餘式定理
餘式定理因此,我們得到了 餘數定理:多項式 除以 所得的餘數等於
 餘式定理
餘式定理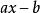 餘式定理
餘式定理 餘式定理
餘式定理推論:多項式除以的餘式為。
關於如何求f(x)除以一個多項式的餘式——長除法 。
特殊的餘式定理——因式定理
1.因式定理的定義
 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理在代數, 因式定理( factor theorem)是關於一個多項式的因式和零點的定理。這是一個 餘式定理的特殊情形。 因式定理指出,一個多項式有一個因式若且唯若。
2.多項式的因式分解
因式定理普遍套用於找到一個多項式的因式或多項式方程的根的兩類問題。從定理的推論結果,這些問題基本上是等價的。
若多項式已知一個或數個零點,因式定理也可以移除多項式中已知零點的部分,變成一個階數較低的多項式,其零點即為原多項式中剩下的零點,以簡化多項式求根的過程。方法如下 :
 餘式定理
餘式定理 餘式定理
餘式定理1)先設法找出多項式的一個零點。
 餘式定理
餘式定理 餘式定理
餘式定理2)利用因式定理確認是多項式的因式。
 餘式定理
餘式定理3)利用長除法計算多項式。
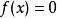 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理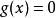 餘式定理
餘式定理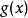 餘式定理
餘式定理 餘式定理
餘式定理 餘式定理
餘式定理4)中,所有滿足條件的根都是方程式的根。因為的多項式階數較要小。因此要找出多項式的零點可能會比較簡單。
5)欲使A=BQ+R成立,就令除式BQ=0,則被除式A=R能使此方程式成立,則被除式=(商式)(除式)+餘式或被除式/除式=商式+餘式/除式。