正文
採樣過程所應遵循的規律，又稱取樣定理、抽樣定理。採樣定理說明採樣頻率與信號頻譜之間的關係，是連續信號離散化的基本依據。採樣定理是1928年由美國電信工程師H.奈奎斯特首先提出來的，因此稱為奈奎斯特採樣定理。1933年由蘇聯工程師科捷利尼科夫首次用公式嚴格地表述這一定理，因此在蘇聯文獻中稱為科捷利尼科夫採樣定理。1948年資訊理論的創始人C.E.香農對這一定理加以明確地說明並正式作為定理引用，因此在許多文獻中又稱為香農採樣定理。採樣定理有許多表述形式，但最基本的表述方式是時域採樣定理和頻域採樣定理。採樣定理在數字式遙測系統、時分制遙測系統、信息處理、數字通信和採樣控制理論等領域得到廣泛的套用。
時域採樣定理頻帶為
的連續信號
(
)可用一系列離散的採樣值
(
),
(
±Δ
)，
(
±2Δ
)，...來表示,只要這些採樣點的時間間隔Δ
≤1/2
，便可根據各採樣值完全恢復原來的信號
(
)。
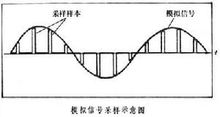
採樣定理時域採樣定理的另一種表述方式是：當時間信號函式
(
)的最高頻率分量為
時,
(
)的值可由一系列採樣間隔小於或等於1/2
的採樣值來確定,即採樣點的重複頻率
≥2
。圖為模擬信號和採樣樣本的示意圖。
時域採樣定理是採樣誤差理論、隨機變數採樣理論和多變數採樣理論的基礎。
頻域採樣定理對於時間上受限制的連續信號
(
)（即當│
│>
時,
(
)=0,這裡
=
-
是信號的持續時間），若其頻譜為
（
）,則可在頻域上用一系列離散的採樣值
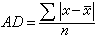採樣定理來表示,只要這些採樣點的頻率間隔
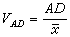採樣定理。
相關公式
採樣定理理想低通信道的最高碼元傳輸速率B=2W Baud (其中W是頻寬)
理想信道的極限信息速率（信道容量）。
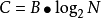採樣定理( bps )
