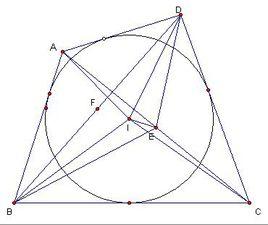
定理1
完全四邊形三條對角線中點共線。
證明：
四邊形ABCD,AB∩CD=E,AD∩BC=F,BD中點M,AC中點L,EF中點N
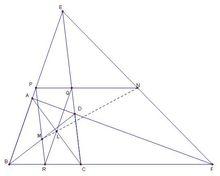牛頓定理1取BE中點P,BC中點R,PN∩CE=QR,L,Q共線
QL/LR=EA/AB
M,R,P共線
RM/MP=CD/DE
N,P,Q共線
PN/NQ=BF/FC
三式相乘得:
QL/LR*RM/MP*PN/NQ=EA/AB*CD/DE*BF/FC
由梅涅勞斯定理
QL/LR*RM/MP*PN/NQ=1
由梅涅勞斯定理的逆定理知:L,M,N三點共線
證畢
故牛頓定理1成立
定理2
圓外切四邊形的兩條對角線的中點，及該圓的圓心，三點共線。
證明：
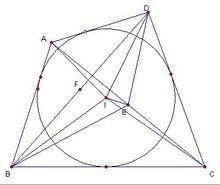牛頓定理2圖設四邊形ABCD是⊙I的外切四邊形，E和F分別是它的對角線AC和BD的中點，連線EI只需證它過點F，即只需證△BEI與△DEI面積相等。顯然，S△BEI=S△BIC+S△CEI-S△BCE，而S△DEI=S△ADE+S△AIE-S△AID。
注意兩個式子，由ABCD外切於⊙I，AB+CD=AD+BC，S△BIC+S△AID=1/2*S四邊形ABCD，S△ADE+S△BCE=1/2*S△ACD+1/2*S△ABC=1/2*S四邊形ABCD
即S△BIC+S△AID=S△ADE+S△BCE，移項得S△BIC-S△BCE=S△ADE-S△AID，由E是AC中點，S△CEI=S△AEI，故S△BIC+S△CEI-S△BCE=S△ADE+S△AIE-S△AID，即S△BEI=△DEI，而F是BD中點，由共邊比例定理EI過點F即EF過點I，故結論成立。
證畢。
定理3
圓的外切四邊形的對角線的交點和以切點為頂點的四邊形對角線交點重合。
證明：
設四邊形ABCD的邊AB,BC,CD,DA與內切圓分別切於點E,F,G,H. 首先證明,直線AC,EG,FH交於一點.設EG,FH分別交AC於點I,I'.顯然∠AHI‘=∠BFI ’
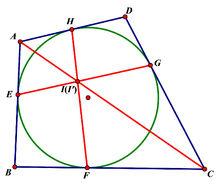牛頓定理因此易知 AI'*HI'/FI'*CI'=S(AI'H)/S(CI'F)=AH*HI'/CF*FI'
故 AI'/CI'=AH/CF.
同樣可證:AI/CI=AE/CG
又AE=AH,CF=CG.
故AI/CI=AH/CF=AI'/CI'.
從而I,I'重合.即直線AC,EG,FH交於一點.
同理可證:直線BD,EG,FH交於一點.
因此直線AC,BD,EG,FH交於一點.
證畢。
