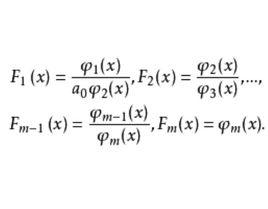基本介紹
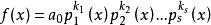分離重因式法
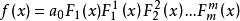分離重因式法設 是f(x)的標準分解式，且其中不可約因式的最高重數m>1。令F(x)為f(x)的一切i重因式之積(i=1，2，…，m)，若f(x)中沒有j重因式，就令F(x)=1。於是由f(x)的標準分解式得 。按以下的方法，可以具體地求出F(x)，F(x)，…，F(x)，令
d(x)=(f，f′)=F(x)F²(x)…F (x)，
d(x)=(d，d′)=F(x)F²(x)…F (x)，
………………………………………
d(x)=(d，d′)=F(x)，
d(x)=1，
則
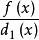分離重因式法φ(x)= =aF(x)F(x)…F(x)，
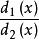分離重因式法φ(x)= =F(x)F(x)…F(x)，
………………………………………
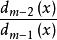分離重因式法φ(x)= =F(x)F(x)，
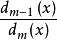分離重因式法φ(x)= =F(x).
於是
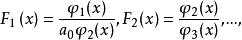分離重因式法
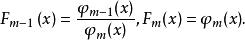分離重因式法這種按以上方法和步驟求出F(x)的方法，稱為 分離重因式法，亦稱 重因式的分離 。
相關定理
定理1 若不可約多項式p(x)是f(x)的k重因式（k≥1），則它是f'(x)的k-1重因式。特別地，f(x)的單因式不是f'(x)的因式。
此定理的逆命題不成立。
定理 次數大於0的多項式f(x)沒有重因式的充分必要條件是f(x)與f'(x)互素 。
證明 設f(x)是一個n(n>0)次多項式，其典型分解式為：
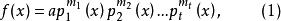分離重因式法由定理1有
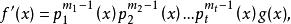分離重因式法此處g(x)不能被任何p(x)（i=1，2，…，t）整除，由求最大公因式的方法，得
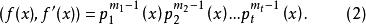分離重因式法
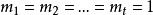分離重因式法 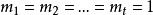分離重因式法因此，若f(x)沒有重因式，亦即 ，從而f(x)與f'(x)互素，反之，若f(x)與f'(x)互素，必有 ，則f(x)沒有重因式．
此定理給出了判斷一個多項式有無重因式的實際方法，即通過輾轉相除法便可解決。
由於多項式的導數以及兩個多項式的最大公因式不因數域的擴大而改變，所以一個多項式有無重因式，也不會因數域的擴大而改變。
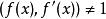分離重因式法
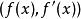分離重因式法如果f(x)有重因式，則 ，由(1)與(2)可以看出，用 去除f(x)所得商式為
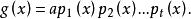分離重因式法g(x)是一個沒有重因式的多項式，且它與f(x)有完全相同的不可約因式。這種去掉因式重數的方法稱為分離重因式法，由於g(x)的次數低於f(x)的次數，所以g(x)的不可約
因式可能比較容易求出，如果已經知道g(x)的一個不可約因式，那么決定它在f(x)中的重數並不難，只要套用帶餘除法就可以計算出來，此方法既然可以求出重因式，故在某些情況下，可以用來分解因式 。
