定理簡介
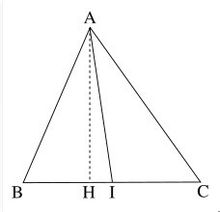
中線定理定理內容：三角形一條中線兩側所對邊平方和等於底邊的一半平方與該邊中線平方的和的2倍。
即，對任意三角形△ABC，設是I線段BC的中點，AI為中線，則有如下關係：
AB+AC=2BI+2AI
或作AB+AC=BC/2+2AI
概述
三角形的三條中線交於一點，這點到頂點的距離是它到對邊中點距離的2倍
證明
中線定理即為斯台沃特定理在中點時的結論，可由斯台沃特定理直接得出，但是斯台沃特定理不容易理解，昏頭昏腦。下面有四種比較容易理解的方法。
第一種
以中點為原點，在水平和豎直方向建立坐標系，
設：A(m,n),B(-a,0),C(a,0)，
則：AD²+CD²=m²+n²+a²
AB²+AC²=(m+a)²+n²+(m-a)²+n²=2(m²+a²+n²)
∴AB²+AC²=2AD²+2CD²
第二種
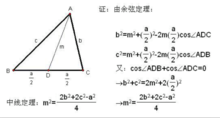
中線定理如圖，利用餘弦定理來證明。
第三種
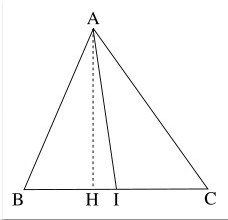
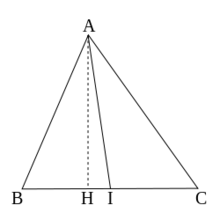
中線定理如圖，AI是△ABC的中線，AH是高線。利用勾股定理來證明。
在Rt△ABH中，有AB²=AH²+BH²
同理，有AI²=AH²+HI²，AC²=AH²+CH²
並且BI=CI
那么，AB²+AC²
=2AH²+BH²+CH²
=2(AI²-HI²)+(BI-IH)²+(CI+IH)²
=2AI²-2HI²+BI²+IH²-2BI×IH+CI²+IH²+2CI×IH
=2AI²+2BI²
第四種
向量法證明中線定理。
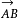中線定理如圖，AI是△ABC的中線，分別取向量
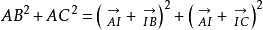中線定理則
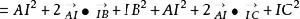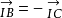中線定理
中線定理注意到
並且
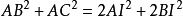中線定理∴得
證明方法
中線定理即為斯台沃特定理在中點時的結論，可由斯台沃特定理直接得出，但是斯台沃特定理不容易理解，昏頭昏腦。
除圖示給出的方法外，lonelystar在此給出另外的兩種常規證明方法
第一種
以中點為原點，在水平和豎直方向建立坐標系，
設：A(m,n),B(-a,0),C(a,0)，
則：(AD)^2+(CD)^2=m^2+n^2+a^2
(AB)^2+(AC)^2=(m+a)^2+n^2+(m-a)^2+n^2=2(m^2+a^2+n^2)
∴(AB)^2+(AC)^2=2((AD)^2+(CD)^2)
第二種
在不同三角形中，對同一個角用兩次餘弦定理，比如對圖示中的∠B（或者∠C）在△ABD和△ABC（或者△ACD和△ABC）使用餘弦定理，從而直接得到三角形邊長的關係，進而得證。
此外，對任意三角形，設是線段的中點，為中線，則有如下關係：
或作
用萊布尼茨標量函式約簡，可以容易導出這性質：只需要在兩個平方中引入：
得出
是的中點，因此和相反，可知式中兩個標積抵消。又因，得出
第三種
或者直接採用勾股定理，過AD點作BC的垂線，垂足為H.
則AD^2=DH^2+AH^2
AB^2=（BD+DH）^2+AH^2
AC^2=（CD-DH）^2+AH^2
∴(AB)^2+(AC)^2=2((AD)^2+(CD)^2)
另一結論
在以上討論中，通過兩式相減，還可以得到|AB^2-AC^2|=2BC×IH。（H為垂足）
