 商空間書籍
商空間書籍定義
假設 X 是一個拓撲空間,~ 是 X 上一個等價關係。在商集合 X/~ (這個集合有所有 ~ 的等價類組成)上定義一個拓撲如下:X/~ 中一個等價集合是開集若且唯若他們的並集在 X 中是開集。所得的拓撲稱為在商集合 X/~ 上的商拓撲(quotient topology)。
等價地,商拓撲可以如下方式刻畫:設 q : X → X/~ 是投影映射,將 X 的任何元素映為它的等價類。則 X/~ 上的商拓撲是使 q 連續的最細拓撲(finest topology)。
給定一個滿射 f : X → Y 從一個拓撲空間 X 到一個集合 Y,我們可以在 Y 上定義商拓撲為使 f 連續的最細拓撲。這等價於說集合 V ⊆ Y 在 Y 中開若且唯若它的原像 f−1(V) 在 X 中開。映射 f 在 X 上誘導了一個等價關係,即 x1~x2 若且唯若 f(x1) = f(x2)。這個商空間 X/~ 同胚於 Y(帶著它的商拓撲),同構映射為將 x 的等價類映為 f(x)。
一般地,一個滿連續映射 f : X → Y 稱為一個商映射(quotient map)如果 Y 具有由 f 確定的商拓撲。
拓撲
黏合:通常,拓撲學家討論將一些點黏合在一起。如果 X 是一個拓撲空間,點 “黏合”在一起,這意味著我們考慮由等價關係 a~b 若且唯若 a = b 或 a = x,b = y(或 a = y,b = x) 得到的商空間。即這兩個點被看作一個。 考慮一個單位正方形 I2 = [0,1]×[0,1] 以及由所有邊界點等價生成的等價關係 ~ ,從而所有邊界點等同到一個等價類。則 I2/~ 同構於單位球面 S2。 黏著空間(Adjunction space):更一般地,假設 X 是一個空間,A 是 X 的一個子空間。我們可以將 A 中所有點等同到一個等價類其餘 A 以外的點不變。所得的空間記作 X/A。2 維球面同構於將單位圓盤的邊界等同為一個點 D2/∂D2。
考慮集合 X = R',取通常拓撲的實數集,記 x ~ y 若且唯若 x−y 是一個整數。則商空間 X/~ 同構於單位圓周 S1,同構映射為將 x 的等價類映為 exp(2πix)。
上一個例子的一類大量的推廣如下:假設一個拓撲群 G 連續作用在空間 X 上。我們可以構造 X 上一個等價關係,如果兩點等價若且唯若它們在同一個軌道中。這個關係下的商空間稱為軌道空間,記作 X/G。上一個例子中 G = Z 通過平移作用在 R 上。軌道空間 R/Z 同構於 S1。
註:記號 R/Z 有歧義:如果 Z 理解成一個群作用在 R 上則商空間是圓周;如果 Z 看作 R 的一個子空間,則商空間是無窮的一束圓(bouquet of circles)在同一個點聯接起來。
性質
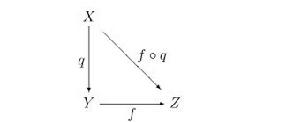
商映射 q : X → Y 是由如下性質刻畫的滿射:如果 Z 是任何拓撲空間,f : Y → Z 是任何函式,則 f 連續當且僅
 商空間
商空間商空間 X/~ 與商映 q : X → X/~ 一起由如下泛性質刻畫。如果 g : X → Z 是一個連續映射使得:對所有 a 與 b 屬於 X, a~b 蘊含 g(a)=g(b) ,則存在惟一連續映射 f : X/~ → Z 使得 g = f O q。我們稱 g “下降到商”。
因此定義在 X/~ 商的連續映射恰是由定義在 X 上與等價關係一致的連續映射(它們將同一個等價類中的元素映到相同的像)誘導的。在研究商空間時,時常使用這個判據。
給定一個連續滿射 f : X → Y,關於 f 是否為商映射的判據是有用的。兩個充分條件是 f 為開映射或閉映射。注意這兩個條件只是充分條件而不是必要的。容易構造出不開或不閉的商映射例子。
相容性
與其它拓撲概念的相容性
分離
一般地,商空間關於分離公理的表現都很壞。X 的分離性質不必被 X/~ 繼承,而 X/~ 可能具有 X 所沒有的分離性質。
X/~ 是一個T1空間若且唯若 ~ 的任何等價類在 X 中閉。
如果商映射開則 X/~ 是一個豪斯多夫空間若且唯若 ~ 是乘積空間 X×X 的一個子集。
連通性
如果一個空間是連通的或道路連通,則所有的商空間也是。
一個單連通或可縮空間的商空間不必具有同樣的性質。
緊性
如果一個空間緊,則所有商空間也是。
一個局部緊空間的商空間不必是局部緊的。
維數
一個商空間的拓撲維數可能比原空間大(顯然也可能比較小),皮亞諾曲線(space-filling curve)提供了這樣的例子。
套用
套用線性空間的第二同構定理,我們可得線性代數中的一個著名維數公式.
定理3.1 設W1,W2是有限維線性空間V的兩個子空間,則 dim(W1+W2)=dimW1+dimW2-dim(W1∩W2).證明:由定理2.7,(W1+W2)∕W2≌W1∕(W1∩W2),於是dim((W1+W2)∕ W2)=dim(W1∕(W1∩W2)). 由命題1.3知dim(W1+W2)-dim W2=dimW1-dim(W1∩W2).
套用線性空間的同態基本定理,我們可得線性代數中的另一個著名的維數公式.
定理3.2 設f是數域P上線性空間V到V’的同態映射,dimV=n,則 dim ker f+dim Im f =n .
證明:由推論2.6,Im f ≌V∕kerf,於是dim Im f=dim(V∕ker f).由命題1.3,可得
dim Im f =n-dim ker f.
註:定理3.1與3.2用傳統的方法(參見一些高等代數、線性代數教材)來證明則比較繁雜,在這裡我們看到,它們本質上是第一、二同構定理的直接推論.
定理3.2有兩個有用的推論:
推論3.3 設V是數域P上有限維線性空間,σ、τ是V上的自同態(線性變換),則 dim Im(στ)=dim Im(τ)-dim(Im(τ)∩ker(σ)).
證明:將σ限制在子空間Im(τ)上,知σ| Im(τ)是Im(τ)到V的一個同態映射,由定理3.2,
dim(ker(σ)∩Im(τ))+dim Im(στ)=dim Im(τ).
推論3.4 設A, B是數域P上m×n, n×M矩陣,則 r(AB)= r(B)-dim(R(B)∩N(A)) = r(A)-dim(R(AT)∩N(BT))這裡R(B)={X | BY=X,Y∈PS},N(A)={X | AX=0,X∈Pn}是Pn的子空間,r(A)為A的秩.
證明:將A限制在子空間R(B)上,則A可看成R(B)到R(A)的一個同態映射,其像為R(AB),核為R(B)∩N(A),於是由定理3.2,
dim(R(B)∩N(A))+dim R(AB)=dim R(B).
由於dim R(AB)=r(AB),dim R(B)=r(B),故有:
r(AB)=r(B)-dim(R(B)∩N(A)).……………………(*)
因為r(AB)=r((AB)T)=r(BT AT),r(A)=r(AT),將BT AT套用到(*)式,可得:
r(AB)=r(A)-dim(R(AT)∩N(BT)).
利用推論3.3和3.4,可證明一些著名不等式.
例1 證明Sylvester不等式
r(A)+r(B)-n≤r(AB)≤min{ r(A),r(B)},
其中A為n列,B為n行.
證明:由推論3.4,有r(AB)=r(B)-dim(R(B)∩N(A)). 因為n-r(A)=dim N(A)≥dim(R(B)∩N(A))≥0,所以
r(AB)=r(B)-dim(R(B)∩N(A))
≥r(B)-(n-r(A))
=r(A)+r(B)-n.
又由推論3.4,顯然有r(AB)≤r(B),r(AB)≤r(A).
例2 證明Frobenius不等式
r(ABC)≥r(AB)+r(BC)-r(B).
證明:由推論3.4,
r(ABC)=r(BC)-dim(R(BC)∩N(A)),
r(AB)=r(B)-dim(R(B)∩N(A)),
兩式相減得:
r(ABC)=r(AB)+r(BC)-r(B)+dim(R(B)∩N(A))-dim(R(BC)∩N(A)).因為R(BC) R(B),所以dim(R(B)∩N(A))-dim(R(BC)∩N(A))≥0,因此
r(ABC)≥r(AB)+r(BC)-r(B).
例3 設σ,τ都是數域P上n維線性空間V上的線性變換,證明
dim ker(στ)≤dim ker(σ)+dim ker(τ).
證明:由定理3.2及推論3.3,
dim Im(στ)=dim Im(τ)-dim(Im(τ)∩ker(σ)),
dim Im(στ)+dim ker(στ)=n,
dim Im(τ)+dim ker(τ)=n。
於是,有
dim ker(στ)=dim ker(τ)+dim(Im(τ)∩ker(σ))。
≤dim ker(τ)+dim ker(σ)。
例4 設σ是數域P上n維線性空間V上的線性變換,證明
dim Im(σ2)=dim Im(σ)若且唯若Im(σ) ker(σ)=V。
證明:由推論3.3,dim Im(σ2)=dim Im(σ)-dim(Im(σ)∩ker(σ)),於是dim Im(σ2)=dim Im(σ)若且唯若dim(Im(σ)∩ker(σ))=0,若且唯若Im(σ)∩ker(σ)={0}。 又由定理3.2,dim Im(σ)+dim ker(σ)=n,故可得dim Im(σ2)=dim Im(σ)若且唯若Im(σ) ker(σ)=V。
