皮亞諾曲線的發現
皮亞諾(Peano)曲線是一條能夠填滿正方形的曲線。
 皮亞諾曲線
皮亞諾曲線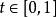 皮亞諾曲線
皮亞諾曲線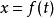 皮亞諾曲線
皮亞諾曲線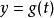 皮亞諾曲線
皮亞諾曲線1890年,義大利數學家皮亞諾(Giuseppe Peano)發現能填滿一個正方形的曲線,叫做皮亞諾曲線。皮亞諾對區間上的點和正方形上的點的對應作了詳細的數學描述。實際上,正方形的這些點對於 ,可規定兩個連續函式 和 ,使得x和y取屬於單位正方形的每一個值。 後來,希爾伯特作出了這條曲線。
維數的認識
在傳統概念中,曲線的維數是1維, 正方形是2維。按照通常的理解,沒有寬度的一維的曲線是不可能填滿2維的方格的。
皮亞諾曲線說明我們對維數的認識是有缺陷的,有必要重新考察維數的定義。這就是分形幾何考慮的問題。在分形幾何中, 維數可以是分數的叫做分數維度。
此外皮亞諾曲線是連續的但處處不可導的曲線。因此如果我們想要研究傳統意義上的曲線, 就必須加上可導的條件,以便排除像皮亞諾曲線這樣的特例。
集合論觀點
 皮亞諾曲線
皮亞諾曲線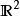 皮亞諾曲線
皮亞諾曲線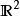 皮亞諾曲線
皮亞諾曲線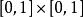 皮亞諾曲線
皮亞諾曲線與 均為不可數集,且基數均為連續統基數。對於 的方塊 ,存在一個一一映射
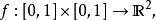 皮亞諾曲線
皮亞諾曲線同理存在一個一一映射
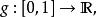 皮亞諾曲線
皮亞諾曲線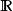 皮亞諾曲線
皮亞諾曲線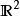 皮亞諾曲線
皮亞諾曲線由於 與 基數相同,故存在一個一一映射
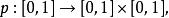 皮亞諾曲線
皮亞諾曲線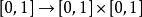 皮亞諾曲線
皮亞諾曲線但該映射不一定是連續的。Peano曲線給出了一個 的連續滿射,一般來說,一維的曲線是不可能填滿2維的方格的。但是皮亞諾曲線恰恰給出了可行的例子。
數學分類導航
| 數學是研究現實世界中數量關係和空間形式的科學。簡單地說,是研究數和形的科學。由於生活和勞動上的需求,即使是最原始的民族,也知道簡單的計數,並由用手指或實物計數發展到用數字計數。基礎數學的知識與運用總是個人與團體生活中不可或缺的一塊。其基本概念的精煉早在古埃及、美索不達米亞及古印度內的古代數學文本內便可觀見。從那時開始,其發展便持續不斷地有小幅的進展,直至16世紀的文藝復興時期,因著和新科學發現相作用而生成的數學革新導致了知識的加速,直至今日。 | |||
| 代數 | 函式 | 級數 | 定理 |
| 方程 | 幾何學 | 數學家 | 統計學 |
| 博弈論 | 數學史 | 範疇論 | 速算 |
| 套用數學 | 離散數學 | 數學軟體 | 數理邏輯 |
| 數學書籍 | 數學猜想 | 數學競賽 | 拓撲學 |
| 數學研究所 | 數學組織 | 數學獎項 | 數學中未解決的問題 |

