定義
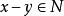 商空間
商空間 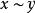 商空間
商空間 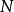 商空間
商空間 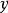 商空間
商空間  商空間
商空間 設 V是域 K上的一個向量空間,且 N是 V的一個子空間。我們定義在 V上定義一個等價類,如果 則令 。即如果其中一個加上 中一個元素得到另一個,則 與 相關。 的所在等價類通常記作
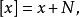 商空間
商空間 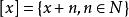 商空間
商空間 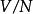 商空間
商空間 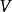 商空間
商空間  商空間
商空間  商空間
商空間 因為它由 給出。那么商空間 定義為 / , V在 下所有等價類集合。等價類上的數乘與加法定義為:
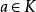 商空間
商空間 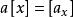 商空間
商空間 1) 對所有 , ,
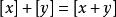 商空間
商空間 2) 。
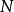 商空間
商空間 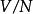 商空間
商空間 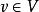 商空間
商空間 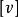 商空間
商空間 不難驗證這些運算是良定義的(即與代表元之選取無關)。這些運算將商空間 轉化為 K上一個向量空間, 成為零類。相對應的,商映射即定義為 與等價類 之映射
性質
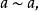 商空間
商空間 (1)反身性:
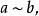 商空間
商空間 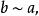 商空間
商空間 (2)對稱性: 若 則
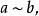 商空間
商空間 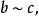 商空間
商空間 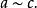 商空間
商空間 (3)傳遞性: 若 則
性質推廣
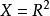 商空間
商空間 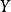 商空間
商空間  商空間
商空間 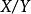 商空間
商空間 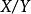 商空間
商空間 令 為標準笛卡兒平面, 是 中過原點的一條直線。則商空間 可與 X中與 Y平行的所有直線等價。這就是講,集合 的元素是 X中平行於 Y的元素。這給出了以一種幾何的方式看 商空間的方法。
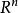 商空間
商空間 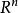 商空間
商空間  商空間
商空間  商空間
商空間 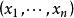 商空間
商空間 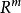 商空間
商空間  商空間
商空間 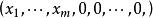 商空間
商空間  商空間
商空間 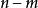 商空間
商空間 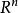 商空間
商空間 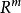 商空間
商空間 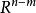 商空間
商空間 另一個例子是 被前 個標準基向量張成的子空間的商。空間 R有所有實數 元組 組成。子空間,與 等價,由只有前 元素是非零 的所有 元組組成。 的兩個向量在模去這個子空間的同一個共軛類中若且唯若他們的後 個坐標相等。商空間 / 顯然地同構於 。
更一般地,如果 V寫成子空間 U與 W的一個(內部)直和:
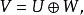 商空間
商空間 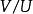 商空間
商空間 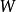 商空間
商空間 則商空間 自然同構於 。
如果 U是 V的一個子空間, U在 V中的余維數定義為 V/ U的維數。如果 V是有限維的,這就是 V與 U的維數之差:
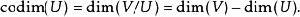 商空間
商空間  商空間
商空間  商空間
商空間 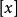 商空間
商空間 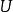 商空間
商空間 從 到商空間 有一個自然滿射,將 x送到它的等價類 。這個滿射的核(或零空間)是子空間 。此關係簡單地總結為短正合序列:
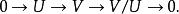 商空間
商空間 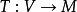 商空間
商空間 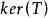 商空間
商空間 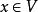 商空間
商空間 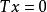 商空間
商空間 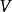 商空間
商空間 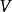 商空間
商空間 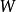 商空間
商空間 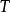 商空間
商空間 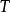 商空間
商空間 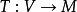 商空間
商空間 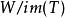 商空間
商空間 線性運算元 的余核定義為商空間 。
商空間
定義
如果 X是一個巴拿赫空間而 M是 X的一個閉子空間,則商 X/ M仍是一個巴拿赫空間。上一節已經給出商空間一個向量空間結構。我們定義 X/ M上一個範數為
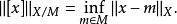 商空間
商空間 商空間 X/ M關於此範數是完備的,所以是一個巴拿赫空間。
例子
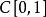 商空間
商空間 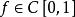 商空間
商空間 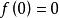 商空間
商空間 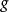 商空間
商空間 令 表示區間[0,1]上連續實值函式的巴拿赫空間。記所有函式 使得 的子空間為 M。則某個函式 的等價類由它在0點的值決定,商空間 C[0,1]/ M同構於 R。
如果 X是一個希爾伯特空間,則商空間 X/ M同構於 M的正交補 。
局部凸空間
 商空間
商空間 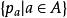 商空間
商空間  商空間
商空間 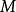 商空間
商空間 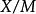 商空間
商空間 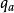 商空間
商空間 局部凸空間被一個閉子空間商還是局部凸的。事實上,假設 是局部凸的所以 上的拓撲由一族半範數 生成,這裡 是一個指標集。設 是一個閉子空間,定義 上半範數
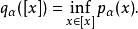 商空間
商空間 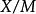 商空間
商空間 則 是一個局部凸空間,上面的拓撲是商拓撲。
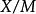 商空間
商空間 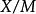 商空間
商空間 進一步,若 X是可度量化的,則 也是;如果 X是弗雷歇空間, 也是。

