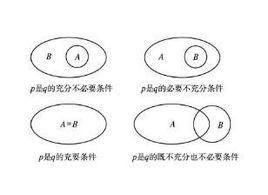
常用定義
對於兩個命題p、q,如果p ⇒q且q ⇒p,則稱p是q的充分必要條件,簡稱充要條件,也稱p與q等價。記作A ⇔B。
集合中的等價關係
定義
若關係R在集合A中是自反、對稱和傳遞的,則稱R為A上的等價關係。所謂關係R 就是笛卡爾積 A×A 中的一個子集。
A中的兩個元素x,y有關係R,如果(x,y)∈R。我們常簡記為 xRy。
自反: 任意x屬於A,則x與自己具有關係R,即xRx;
對稱: 任意x,y屬於A,如果x與y具有關係R,即xRy,則y與x也具有關係R,即yRx;
傳遞: 任意x,y,z屬於A,如果xRy且yRz,則xRz
x,y具有等價關係R,則稱x,y R等價,有時亦簡稱等價。
舉例
例如:在全體人的集合A中,室友是A上的一種關係,如果認為自己跟自己可以稱為室友,則滿足自反性,但如果甲是乙的室友,則必定乙是甲的室友,滿足對稱性,同時,如果甲是乙的室友,乙是丙的室友,則甲是丙的室友,滿足傳遞性;因此,室友關係可以稱為等價關係。於是在代表宿舍參加活動這一點上,宿舍成員身份是等同的,不論甲還是乙,對外不加區別,即甲乙等價。
其他等價的定義
另外,三角形的全等也是等價關係。因為A全等A;A全等B=>B全等A;A全等B,B全等C=>A全等C。
A中與元素 x 等價的所有元素構成的子集叫做 x 所在等價類, x也稱為這個等價類的代表元。 集合A可以劃分為一些等價類的並集,這些等價類兩兩不相交。 任何元素都必定落在某個等價類裡面。
更廣泛意義的等價,是集合在某種變換下保持不變性。如:矩陣A與稱為等價的,如果B可以是A經過一系列初等變換得到。矩陣在初等變換下是行列式不變的。線上性代數中,契約、相似都是等價關係。