十八世紀數學
正文
微積分學深入發展，是18世紀數學的主要線索。這種發展與廣泛的套用緊密交織在一起，刺激和推動了許多新分支的產生，使分析形成了在觀念和方法上都具有鮮明特點的獨立的數學領域。在18世紀特別是後期，數學研究活動和數學教育方式也發生了變革。這一切，使18世紀成為向現代數學過渡的重要時期。微積分的發展 無限小算法的推廣，在英國和歐洲大陸國家是循著不同的路線進行的。
不列顛數學家們在劍橋、牛津、倫敦、愛丁堡等著名的大學裡傳授和研究I.牛頓的流數術，他們中的優秀代表有R.科茨、B.泰勒、C.馬克勞林、A.棣莫弗和J.斯特林等。泰勒發現的著名公式
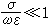
泰勒、馬克勞林之後，英國數學陷入了長期停滯、僵化的狀態。18世紀初即已爆發的微積分發明權的爭論，滋長了不列顛數學家們濃厚的民族保守情緒，他們囿於牛頓的傳統，不能擺脫其迂迴的幾何手法等弱點的束縛。與此相對照，在海峽的另一邊，新分析卻在G.W.萊布尼茨的後繼者們的推動下蓬勃發展起來。
推廣萊布尼茨學說的任務，從17世紀向18世紀過渡的時候，主要由他的學生、瑞士巴塞爾的雅各布第一·伯努利和約翰第一· 伯努利（見伯努利家族）兩兄弟擔當，而這方面最重大的進步則是由L.歐拉作出的。歐拉於1748年出版了《無窮小分析引論》，這部巨著與他隨後發表的《微分學》(1755)、《積分學》(1768～1774)，標誌著微積分歷史上的一個轉折：以往的數學家們都以曲線作為微積分的主要研究對象，而歐拉則第一次把函式放到了中心的地位──微積分被看作是關於函式的理論,並且是建立在函式的微分的基礎之上。函式概念本身正是由於歐拉等人的研究而大大豐富了。數學家們開始明確區分代數函式與超越函式、隱函式與顯函式、單值函式與多值函式等；通過一些困難積分問題的求解，諸如Γ函式、B函式、 橢圓不定積分等一系列新的超越函式被納入函式的範疇；已有的對數、指數和三角函式的研究不僅進一步系統化而且被推廣到複數領域(著名公式
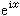
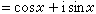的發現)。 在18世紀,數學家們對於函式、導數、微分、連續性和級數收斂性等概念未能形成統一的見解，他們往往不顧基礎問題的困難而大膽前進。儘管如此，許多人對於建立微積分的嚴格基礎仍作出了重要的嘗試。除了歐拉的函式理論外,另一位天才的分析大師J.-L.拉格朗日採取了所謂“代數的途徑”。他在1797年出版的《解析函式論》一書中,主張用泰勒級數來定義導數(函式ƒ(x)的導數ƒ┡(x)被定義為展開式
中i的係數)，以此作為整個微分、積分理論之出發點。 J.le R.達朗貝爾則發展了牛頓的“首末比方法”，但用極限的概念代替了含糊的“最初與最終比”的說法。如果說歐拉和拉格朗日的著作引入了分析的形式化趨勢，那么，達朗貝爾則為微積分的嚴格表述提供了合理的核心。19世紀的嚴格化運動，正是這些不同方向融會發展的結果。
數學同力學的結合與分析新分支的出現 同力學的有機結合，是18世紀數學的另一個鮮明特徵。這種結合，其緊密的程度為數學史上任何時期所不能比擬。幾乎所有的數學家都以巨大的熱情致力於運用微積分新工具去解決各種物理、力學問題。歐拉的名字同流體力學和剛體運動的基本方程聯繫著；拉格朗日最享盛名的著作《分析力學》(1788)，“將力學變成了分析的一個分支”；P.-S.拉普拉斯 (1749～1827)則把數學看作是研究力學、天文學的工具，他的許多重要數學成果正是包含在他的5大卷《天體力學》中。
這種廣泛的套用成為新的數學思想的源泉而使數學本身的發展大大受惠。一系列新的數學分支在18世紀成長起來。
達朗貝爾關於弦振動的著名研究(1747)，導出了弦振動方程
及其最早的解，成為偏微分方程論的發端。另一類重要的偏微分方程─位勢方程 
,
常微分方程的研究進展更為迅速。從17世紀末開始，三體問題、擺的運動及彈性理論等的數學描述引出了一系列的常微分方程，其中以三體問題最為重要，二階常微分方程在其中扮演了中心角色。數學家起先是採用各種特殊的技巧對付不同的方程，但漸漸地開始尋找帶普遍性的方法。這樣,歐拉推廣了約翰第一·伯努利的積分因子和常數變易法（常數變易法在拉普拉斯、拉格朗日的行星攝動論中得到了更充分的發展），黎卡提在以他的名字命名的非線性方程
的研究中首創了後來成為處理高階方程主要手段的降階法；泰勒最先引起人們對奇異解存在性的注意；歐拉在1750年解出了一般的常係數線性方程，他還引進超幾何級數作為解二階線性方程的基礎；對全微分方程的研究亦由歐拉、拉格朗日和G.蒙日等開展起來。 變分法起源於最速降曲線問題和相類似的一些問題，它的奠基人是歐拉。所謂“最速降曲線”問題，是要求出兩點間的一條曲線，使質點在重力作用下沿著它由一點至另一點降落得最快。這問題在1696年被約翰第一·伯努利提出來向其他人挑戰，牛頓、G.-F.-A.de洛必達和伯努利兄弟不久都分別獲得了正確的解答（擺線）。歐拉自1728年開始以他特有的透徹精神重新考察了最速降曲線等問題，最終確立了求積分極值問題的一般方法。歐拉的方法後來又為拉格朗日所發展，拉格朗日首先將變分法置於分析的基礎上，他還充分運用變分法來建造其分析力學體系，全部力學被他化歸為一個統一的變分原理──虛功原理。
這些新的分支與微積分本身一起，形成了被稱之為“分析”的廣大領域，與代數、幾何並列為數學的三大學科，在18世紀，其繁榮程度遠遠超過了代數與幾何。18世紀的數學家們不僅大大拓展了分析的疆域，同時賦予它與幾何相對的意義，他們力圖用純分析的手法以擺脫對於幾何論證的依賴，這種傾向成為18世紀數學的另一大特徵，並且在歐拉和拉格朗日的工作中表現得最為典型。拉格朗日在《分析力學》序中宣稱：“在這本書中找不到一張圖，我所敘述的方法既不需要作圖，也不需要任何幾何的或力學的推理，只需要統一而有規則的代數（分析）運算”。
幾何與代數 對於幾何學，18世紀數學家們著眼於分析方法的套用及與此相聯繫的坐標幾何的發展。雖然早先已有部分結果，但微分幾何形成為獨立的學科主要是在18世紀。伯努利兄弟以及歐拉、拉格朗日等在確定平面曲線曲率、拐點、漸伸線、漸屈線、測地線及曲線簇包絡等方面作出許多貢獻，蒙日自1771年起發表的一系列工作，則使微分幾何在18世紀的發展臻於高峰。蒙日及其學生全面概括了空間曲線的一般理論，並借著偏微分方程對已為歐拉等人觸及的可展曲面、極小曲面、曲面曲率及各種曲面簇等問題獲得了系統的結果。蒙日通過其幾何研究還建立了偏微分方程的特徵理論。
現代解析幾何的基本課題如對稱的坐標軸概念、平面曲線的系統研究等，基本上也是18世紀的產品。Α.帕倫於1705、1713年將解析幾何推廣至三維情形，該項工作被A.-C.克萊羅所繼續。解析幾何突破了R.笛卡兒以來作為求解幾何難題的代數技巧的界限。
對綜合幾何的興趣直到18世紀末才被重新喚起，這主要歸功於蒙日的《畫法幾何學》(1799)。蒙日指出畫法幾何只是投影幾何的一個方面，這促進了更一般的投影幾何學與幾何變換理論的發展。投影幾何在19世紀整整活躍了一個世紀，而幾何變換則已成為現代幾何學的基本概念。
18世紀許多數學家將分析看作代數的延伸，代數本身的研究有時便服從分析的需要。然而18世紀代數學仍為下一世紀的革命性發展開闢了道路。1799年，C.F.高斯發表了關於代數基本定理的研究，他給出了該定理的第一個嚴格證明。高於四次的代數方程用根式求解之不可能,也已被拉格朗日等人認識,拉格朗日在《方程的代數求解》(1798)一文中討論了這個問題，雖未能作出嚴格證明，但卻考察了根的有理函式及根的置換對它們的影響。高斯、拉格朗日的結果是19世紀N.H.阿貝爾、E.伽羅瓦、C.G.J.雅可比等在方程論方面的劃時代成就的出發點。虛數在18世紀數學中的重要性增加了，達朗貝爾關於一切虛數都有形式α+b)i的斷言被大多數同時代的學者所接受（雖然他的論證並不嚴格）；丹麥的C.韋塞爾提出了虛數的圖像表示法(1797)，這一切為19世紀複變函數論的發展奠定了基礎。
機率論的數學基礎 B.帕斯卡、P.de費馬和C.惠更斯以來,第一個對機率論給予認真注意的是雅各布第一·伯努利。他的《猜度術》(1730)一書，包含了大數律的敘述;A.棣莫弗最早使用常態分配曲線(1733);拉格朗日的貢獻則在於誤差理論。不過，首先將機率論建立在堅固的數學原理基礎上的是拉普拉斯。從1771年起，拉普拉斯發表了一系列重要著述，特別是1812年出版的《機率的解析理論》，它們對古典機率論作出了強有力的數學綜合，敘述並證明了許多重要定理。拉普拉斯等人的著作還討論了機率論對人口統計、保險事業、度量衡、天文學甚至某些法律問題的套用。機率論在18世紀已遠不再是只與賭博問題相聯繫的學科了。
數學研究活動與數學教育 18世紀的數學研究活動，大部分是與歐洲各國的科學院相聯繫，尤其是大陸國家的科學院，不只是具有象皇家學會那樣評議研究成果，促進科學通訊的職能，而且掌握著聘用專門成員的財政經費。萊布尼茨1700年創立的柏林科學院，在普魯士國王弗里德里克時代曾擁有歐拉(1741～1766)和拉格朗日(1766～1787)為院士；歐拉其餘的生涯是在彼得堡科學院奉職(1727～1741,1766～1783);拉格朗日在弗里德里剋死後被路易十六請到巴黎，而巴黎科學院也許是18世紀歐洲最重要的學術中心，與它相聯繫的法國最卓越的數學家還有克萊羅、達朗貝爾、孔多塞、拉普拉斯、蒙日以及A.-M.勒讓德等。
這種主要靠宮廷支持的科學院，在推動數學研究職業化方面起了一定的但卻是有限的作用。在18世紀的晚期，人們開始注意並努力改變大學中數學教育與研究分離、脫節的現象。哥廷根大學最先強調教學與研究的結合，但對當時的數學並未發生影響。真正的衝擊是來自法國。法國大革命時期建立的巴黎綜合工科學校(1794)和巴黎高等師範學校（1794初建,1808重建）,不僅提供為培養工程師和教師所必需的數學教育，對數學研究也給予同樣的重視，它們作為新型的科學教育和研究機構的典範，對19世紀數學研究職業化運動有極大的影響。
社會政治對18世紀數學發展的影響值得注意。18世紀數學研究活動中心的轉移，明顯地與資產階級革命中心的轉移現象相吻合。英國學術界的保守氣氛，同擁教保王的政治環境不無關係，而在啟蒙思想薰陶下的法國學派卻自覺地接過了發展牛頓自然科學理論（特別是他所建立的宇宙圖像及數學解釋）的任務。法國大革命本身提供了社會變革影響數學事業的史例。這個國家當時最優秀的數學家，幾乎都被革命政權吸收到度量衡改革、教育改革、軍事工程建設等活動中去。對於數學發展特別重要的是他們在新成立的巴黎綜合工科學校與巴黎高等師範學校中的作用。拉格朗日、拉普拉斯、蒙日、勒讓德等均受聘出任那裡的數學教授，蒙日還是綜合工科學校的積極創建者併兼校長。他們的任職，使這兩所學校特別是綜合工科學校成為新一代數學家的搖籃（如A.-L.柯西和S.-D.泊松都是畢業於綜合工科學校）。這些學校為適應培養新人才的需要而採用的數學新教材，釀成了“教科書的革命”，其中勒讓德的《幾何學基礎》(1794)、蒙日的《畫法幾何學》、拉克魯瓦的《微積分學》(1797)以及J.-B.畢奧和 F.L.勒弗朗索瓦的解析幾何教程，都是反覆再版，並被譯成了多國語言。在法國所進行的改革,到19世紀初即已擴及旁國特別是德國,並刺激了英國數學的復甦，成為數學發展新時代的序幕。
