中央極限定理

中央極限定理，重複地從平均數μ，標準差為σ的母群中抽取樣本大小為N的許許多多樣本，得到許許多多樣本平均數，而這些樣本平均數將成為常態分配，不管原來母群的各分數之次數分配形狀如何，且這些樣本平均數的平均數將等於μ，這些樣本平均數的標準差（特稱為標準誤）將等於σ/√n。

基本信息

• 中文名稱：中央極限定理
• 表達式：σXn^2=（σ^2）/n
• 套用學科：數學
• 適用領域範圍：數學、社會學

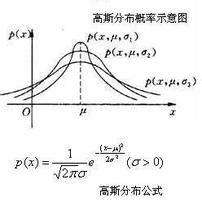
簡介

母

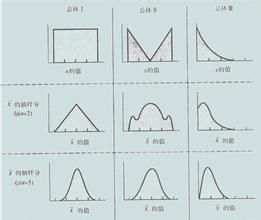中央極限定理

群是一個有著母群平均數μ，標準差σ的母群。我們從該母群中隨機取n多個樣本。這些樣本的平均數用Xn表示。如果按上述過程做一次的話，得到的Xn是一個具體數字。

但Xn實際上也是一個隨機變數。它也有自己的機率分配。我們把這個隨機變數Xn的期待值E(Xn)或平均值表達為μXn，把它的標準差表達為σXn。中央極限定理告訴我們這個隨機變數Xn的分配是常態分配。並且期待值μXn就等於原來母群的平均數μ，標準差也跟原來母群標準差有關，σXn=(σ^2)/n。

意義

中央極限定理以嚴格的數學形式闡明了在大樣本條件下，不論總體的分布如何，樣本的均值總是近似地服從常態分配。如果一個隨機變數能夠分解為獨立同分布的隨機變數序列之和，則可以直接利用中央極限定理進行解決。總之，恰當地使用中心極限定理解決實際問題有著極其重要意義。