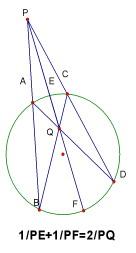
證法1
三角函式證法
在這裡僅考慮二次曲線為圓的情況
連BF、DF、AE、CE
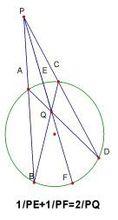 三割線定理
三割線定理由AE內分∠PAQ→由分角定理→
(EQ/PE)=(sin∠EAQ/sin∠PAE)(sin∠APQ/sin∠AQP)
由CE內分∠PCQ→由分角定理→
(EQ/PE)=(sin∠ECQ/sin∠ECP)(sin∠CPQ/sin∠CQP)
由∠EAQ=∠DFE=∠ECP,∠PAE=∠EFB=∠ECQ→
(EQ·EQ)/(PE·PE)=(sin∠APQ·sin∠CPQ)/(sin∠AQP·sin∠CQP)⑴。
由BF外分∠PBQ→
(FQ/PF)=(sin∠FBQ/sin∠PBF)(sin∠APQ/sin∠BQP○)
由DF外分∠PDQ→
(FQ/PF)=(sin∠FDQ/sin∠PDF)(sin∠CPQ/sin∠DQP○)
由∠FBQ與∠PDF,∠PBF與∠FDQ互補,→
(FQ·FQ)/(PF·PF)=(sin∠APQ·sin∠CPQ)/(sin∠CQP○·sin∠AQP○)⑵,(○表示互補)
⑴⑵→EQ/PE=FQ/PF→(PQ-PE)/PE=(PF-PQ)/PF→(PQ/PE)-1=1-(PQ/PF)→
PQ/PE+PQ/PF=2→1/PE+1/PF=2/PQ。證畢。
證法2
幾何證法
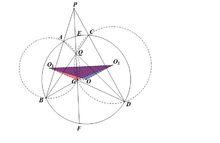 三割線定理
三割線定理在這裡僅考慮二次曲線為圓的情況
在PE上取一點G,使=PQ*PG=PA*PB=PC*PD
易證AQGB共圓,圓心為O1,BCQG共圓,圓心為O2
∵兩圓圓心的連線段垂直於兩圓交點的連線段
∴O1O2⊥PF,O1O⊥PB,O2O⊥PD
∴∠O2O1O=∠BPF,∠O1O2O=∠DPF
易證∠BGQ=∠PCQ=180°-∠BAQ
∴∠QBG=∠DPF,∠GO1O2=∠QBG=∠DPF,同理可得:∠GO2O1=∠BPF
∴∠O2O1O=∠GO2O1,∠O1O2O=∠GO1O2,△O1O2G≌△O1O2O(AAS)
∴四邊形O1O2OG為等腰梯形,OG∥O1O2
又O1O2⊥PB,故OG⊥PB,垂徑定理得:G為EF中點
∴2PG=PE+PF
又PG*PQ=PA*PB=PE*PF,∴2PG*PQ=2PE*PF
∴(PE+PF)*PQ=2PE*PF,等式兩端同時除以PE*PF*PQ得:1/PE+1/PF=2/PQ。證畢。