定理
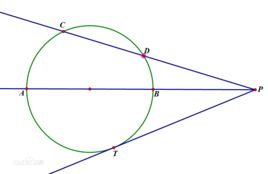
切割線定理：從圓外一點引圓的切線和割線，切線長是這點到割線與圓交點的兩條線段長的比例中項。是圓冪定理的之一。
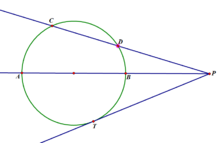切割線定理示意圖幾何語言：∵PT切⊙O於點T，PDC是⊙O的割線
∴PT²=PD·PC（切割線定理）
推論：
從圓外一點引圓的兩條割線，這一點到每條割線與圓的交點的兩條線段長的積相等
幾何語言：∵PT是⊙O切線，PBA、PDC是⊙O的割線
∴PD·PC=PA·PB（切割線定理推論）(割線定理）
由上可知:PT²=PA·PB=PC·PD
證明
切割線定理證明：
設ABP是⊙O的一條割線，PT是⊙O的一條切線，切點為T，則PT^2=PA·PB
證明：連線AT， BT
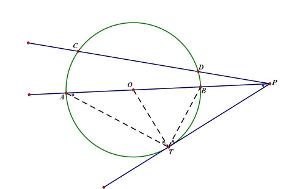切割線定理的證明∵∠PTB=∠PAT(弦切角定理) ∠P=∠P(公共角)
∴△PBT∽△PTA(兩角對應相等，兩三角形相似)
則PB：PT=PT：AP
即：PT^2=PB·PA
比較
相交弦定理、切割線定理及割線定理(切割線定理推論)以及他們的推論統稱為圓冪定理。一般用於求直線段長度。
