定理內容
圓周角的度數等於它所對弧上的圓心角度數的一半。
定理證明
已知在⊙O中,∠BOC與圓周角∠BAC同對弧BC,求證:∠BOC=2∠BAC.
證明:
情況1:
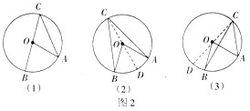
如圖1,當圓心O在∠BAC的一邊上時,即A、O、B在同一直線上時:
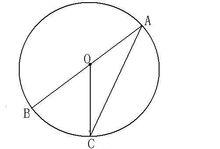 圖1
圖1∵OA、OC是半徑
解:∴OA=OC
∴∠BAC=∠ACO(等邊對等角)
∵∠BOC是△AOC的外角
∴∠BOC=∠BAC+∠ACO=2∠BAC
情況2:
如圖2,,當圓心O在∠BAC的內部時:
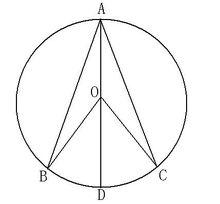 圖2
圖2連線AO,並延長AO交⊙O於D∵OA、OB、OC是半徑
解:∴OA=OB=OC
∴∠BAD=∠ABO,∠CAD=∠ACO(等邊對等角)
∵∠BOD、∠COD分別是△AOB、△AOC的外角
∴∠BOD=∠BAD+∠ABO=2∠BAD(三角形的外角等於兩個不相鄰兩個內角的和)
∠COD=∠CAD+∠ACO=2∠CAD(三角形的外角等於兩個不相鄰兩個內角的和)
∴∠BOC=∠BOD+∠COD=2(∠BAD+∠CAD)=2∠BAC
情況3:
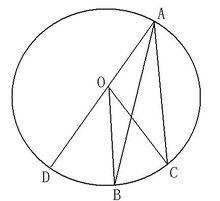 圖3
圖3如圖3,當圓心O在∠BAC的外部時:連線AO,並延長AO交⊙O於D連線OA,OB。
解:∵OA、OB、OC、是半徑
∴OA=OB=OC
∴∠BAD=∠ABO(等腰三角形底角相等),∠CAD=∠ACO(OA=OC)
∵∠DOB、∠DOC分別是△AOB、△AOC的外角
∴∠DOB=∠BAD+∠ABO=2∠BAD(三角形的外角等於兩個不相鄰兩個內角的和)
∠DOC=∠CAD+∠ACO=2∠CAD(三角形的外角等於兩個不相鄰兩個內角的和)
∴∠BOC=∠DOC-∠DOB=2(∠CAD-∠BAD)=2∠BAC
圓心角等於180度的情況呢?
看情況1的圖,圓心角∠AOB=180度,圓周角是∠ACB,
顯然因為∠OCA=∠OAC=∠BOC/2
∠OCB=∠OBC=∠AOC/2
所以∠OCA+∠OCB=(∠BOC+∠AOC)/2=90度
所以2∠ACB=∠AOC
圓心角大於180度的情況呢?
看情況3的圖,圓心角是(360度-∠AOB),圓周角是∠ACB,
只要延長AO交園於點D,由圓心角等於180度的情況可知∠ACD=∠ABD=90度
根據情況3同理可證:∠BOC=2∠BAC=2∠BDC
根據情況1和情況3同理可證:∠AOC=2∠ADC=2∠ABC
所以∠ACB+∠ADB=∠ACB+∠ADC+∠BDC=∠ACB+∠ABC+∠BAC=180度
即∠ACB=180度-∠ADB
由情況2可知:∠AOB=2∠ADB
所以360度-∠AOB=2(180度-∠ADB)=2∠ACB
定理推論
 圓周角圖
圓周角圖1.一條弧所對的圓周角等於它所對的圓心角的一半;
2.圓周角的度數等於它所對的弧度數的一半;
3.在同圓或等圓中,同弧或等弧所對的圓周角相等;相等的圓周角所對的弧也相等。
4.半圓(直徑)所對的圓周角是直角。
5.90°的圓周角所對的弦是直徑。
6.等弧對相等的圓周角。(因為相等的弧只有一個圓心角)
注意:在圓中,同一條弦所對的圓周角有無數個。