證明
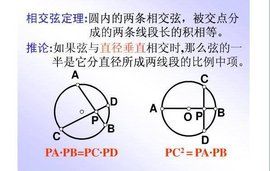
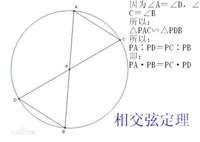
相交弦定理證明：連結AC，BD
由圓周角定理的推論，得∠A=∠D，∠C=∠B。（圓周角推論2: 同(等)弧所對圓周角相等.）
∴△PAC∽△PDB
∴PA∶PD=PC∶PB，PA·PB=PC·PD
註：其逆定理可作為證明圓的內接四邊形的方法. P點若選在圓內任意一點更具一般性。其逆定理也可用於證明四點共圓。
P 不是圓心
比較
相交弦定理、切割線定理及割線定理(切割線定理推論)以及他們的推論統稱為圓冪定理。一般用於求線段長度。
當P點在圓內時稱為相交線定理，當P點在圓上時稱為切割線定理，當P點在圓外時稱為割線定理。三條定理統稱為圓冪定理。其中|OP²-R²|稱為P點對圓O的冪。（R為圓O的半徑）
