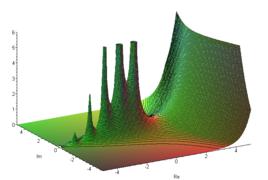
定義
亞純函式（meromorphic function）是在區域D上有定義，且除去極點之外處處解析的函式。
在複分析中，一個複平面的開子集D上的亞純函式是一個在D上除一個或若干個孤立點集合之外的區域全純的函式，那些孤立點稱為該函式的極點。
定義擴展
黎曼曲面上的亞純函式
在一個黎曼曲面上，每個點都擁有一個同構於複平面上的一個開子集的開鄰域。因此，在任意黎曼曲面上都可以定義亞純函式。
當 D為整個黎曼球時，亞純函式域就是複平面上的單變數有理函式域，因為可以證明任意黎曼球上的亞純函式都是有理函式（這是所謂的GAGA原理的一個特例）。
舉例說明
比如有理函式就是在擴充複平面上的亞純函式，它是兩個多項式的商而Q（z）的零點是R（z）的極點，即R（z）有有限多個極點，∞點是R（z）的極點或可去奇點。複平面上不是有理函式的亞純函式稱為超越亞純函式。
例如ctg( z)就是超越亞純函式，它以kπ為全部極點，超越亞純函式一定有無限多個極點。有理函式可以分為部分分式，即其中{ak}是R( z )的全部極點 ，Pk( u )是多項式 ， 當∞點是m階極點時，P0(z)是m階多項式 。
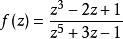亞純函式所有的有理函式如 都是在整個複平面上的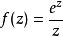亞純函式。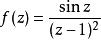
亞純函式
亞純函式函式和以及Γ函式和黎曼ζ函式都是在整個複平面上的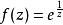亞純函式。
亞純函式函式在除去原點：0的整個複平面上有定義。但是，0不是這個函式的一個極點，而是一個本性奇點。因此，這個函式只是在 C上的亞純函式，而不是在整個複平面上的亞純函式。
函式f(z)=ln z不是在整個複平面上的亞純函式，因為它只在複平面上的一個孤立點集上有定義。
性質
由於亞純函式的極點是孤立點，它們至多有可數多個。極點的個數可以有無窮多個，例如函式：
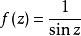亞純函式使用解析拓延來消去可去奇點後，亞純函式可以進行加減法和乘法的運算。當g(z)在 D的連通部分上不恆為零時，還可以定義 f/ g。因此，當 D連通時，所有的亞純函式構成一個域，為複數域的一個域擴張。
擴展知識
複平面上的超越亞純函式也有一個部分分式分解定理 ， f(z)是以{ak}為極點集的超越亞純函式，設f(z)在極點ak處羅朗展式的主部為，Pk(u)是一個多項式，於是f(z)可表作：中g(z)是整函式 ，hk(z)是適當選取的多項式。 對於超越亞純函式有一個類似畢卡定理的結果 ：f(z)是超越亞純函式，則最多除去兩個例外值外 ，對所有其他值W， f(z)－W一定有無窮多個零點。
