函式值分布論
正文
複變函數論中歷史悠久、理論完美的一個分支。初等代數的一個基本問題是求多項式的零點。然而一些理論和實際問題還要求研究較為廣泛的函式類──整函式和亞純函式的取值情況，這便是函式值分布論的主要研究內容。
1879年法國著名數學家(C.-)É.皮卡藉助於模函式證明了：若ƒ(z)為一整函式，且不蛻化為常數，則對於任意複數α（值∞包括在內）,方程ƒ(z)=α都有根，至多除去兩個例外值。皮卡定理是函式論中一個十分深刻的結果,它奠定了值分布論的基礎。以後М.拉蓋爾、（J.-）H.龐加萊等曾經繼續從事研究。J.（-S.）阿達馬建立了整函式與亞純函式的分解定理,並且將其套用於ζ函式的零點的研究。
1896年(F.-É.-J.-) É.波萊爾正式引入整函式的級的概念,把皮卡定理大大推進了一步。他證明了:若ƒ(z)為一整函式，其級ρ是有窮正數，則對於任意複數α有
，
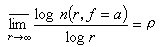20世紀初，有很多學者從事值分布論的研究，其中應特別提到E.L.林德勒夫、L.O.布盧門塔爾、A.當儒瓦、A.威曼、G.瓦利隆、J.E.李特爾伍德等。還有很多研究工作與值分布論密切相關,諸如延森公式,蘭道定理，朔特基定理，關於漸近值的著名的當儒瓦猜測（後來為L.V.阿爾福斯證實），套用廣泛的菲拉格芒－林德勒夫原理，蒙泰爾關於正規族的理論以及F.艾弗森關於反函式的研究等。
1919年G.朱利亞套用蒙泰爾的正規定則證明了：若ƒ(z)為超越整函式，則至少存在一條從原點發出的半直線J:argz=θ0(0≤θ0<2π)，使得對於任意正數ε與所有複數α在角域｜argz-θ0｜<ε內ƒ(z)= α都有根,至多可能除去兩個例外值。這樣的方向稱為ƒ(z)的朱利亞方向。朱利亞定理開創了在一射線附近函式取值情況的研究，這類研究稱為輻角分布論；而在整個平面上函式取值的研究，則稱為模分布論。1924年H.米洛證明了所謂充滿圓的存在，把朱利亞定理向前推進了一步。
1925年，芬蘭數學家R.奈望林納把亞純函式作為主要研究對象，建立了兩個基本定理。他的研究使值分布論呈現了嶄新的面貌，開始了值分布的近代理論（也常常稱為奈望林納理論）。這是對20世紀數學發展的一個重大貢獻。對於亞純函式ƒ(z)和任意複數α,除去量n(r,ƒ=α)外，還可考慮其積分平均值
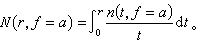
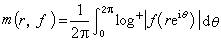而 
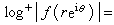
。這時ƒ(z)的級被定義為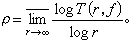 
。
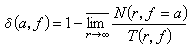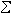δ(α,ƒ)≤2。這個式子稱為虧量關係。 套用奈望林納理論，瓦利隆於1928年將朱利亞方向和充滿圓作了重大發展,證明了波萊爾方向的存在性。若ƒ(z)為ρ(0<ρ<∞)級亞純函式,則至少存在一條從原點出發的半直線B:argz＝θ0(0≤θ0<2π)，使得對於任意正數ε與所有複數α有
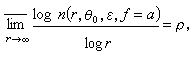
這一階段有很多傑出的學者從事值分布論的研究。除去奈望林納兄弟、瓦利隆、米洛，還有阿爾福斯、A.布洛赫、H.嘉當、M.L.卡特賴特、O.泰希米勒等。值分布論關於例外值的研究實質上等價於函式的黎曼曲面的分支性質的研究。隨著值分布論的發展，就對黎曼曲面的研究提出了一系列問題。這方面奈望林納兄弟和阿爾福斯等學者做了不少工作。
在第二次世界大戰期間以及戰後的幾年裡，函式值分布論的研究較為沉寂。但是從50年代中期以來，這方面的優秀工作又屢有出現。其中A.埃德雷與W.H.I.富克斯、A.A.戈爾德貝格關於亞純函式的虧值與虧量的一系列研究，W.K.海曼關於亞純函式結合於其導數的一個基本不等式，D.德拉辛關於奈望林納理論的反問題的徹底解決以及奈望林納猜想的徹底解決，A.韋茨曼證明了有窮級亞純函式的每個虧量的立方根仍然構成收斂級數等則是其中傑出的代表。1973年，A.伯恩斯坦基於值分布論與傅立葉分析，引進了T*函式，並用以證明了所謂展布關係。以後，T*函式在單葉函式、整函式的最小模等方面也取得了套用。
函式值分布論還被推廣到代數體函式（G.雷蒙多斯、瓦利隆、H.塞爾伯格、E.烏里希），亞純曲線（H.外爾、J.韋爾、阿爾福斯、伍鴻熙）以及多複變函數（陳省身、R.博特、P.格里菲思、W.斯托爾）。圍繞著推廣奈望林納的兩個基本定理與虧量關係，每個方面都有不少研究工作。
在熊慶來的倡導下，莊圻泰、楊樂、張廣厚等從事值分布論的研究，取得了顯著的成果。具有代表性的研究工作有關於無窮級亞純函式值分布的研究，奈望林納第二基本定理的推廣與虧函式，亞純函式虧值數目與波萊爾方向數目的關係，波萊爾方向的分布規律，關於漸近值的研究，亞純函式的輻角分布等。
參考書目
楊樂著：《值分布論及其新研究》,科學出版社,北京，1982。
R.Nevanlinna，Analytic Functions. Springer-Verlag,Berlin,1970.
W.K.Hayman,Meromorphic Functions，Oxford Math.Monographs,Oxford Univ.Press,London,1964.
