概念介紹
代數體函式(algebroidal function)亞純函式或代數函式的推廣。
演算推論
設M為亞純函式域,M[x]表示係數為M的多項式環,則代數體函式域A是M[x]的代數閉包,即任一個w∈A,存在F∈M[x],使得:
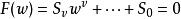 代數體函式
代數體函式其中S(j=0,1,2,…,ν)∈M,或者經通分後w滿足下述不可約方程:
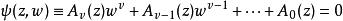 代數體函式
代數體函式其中A(z)(j=0,1,…,ν)是z的整函式(通常考慮A(z)中至少有一個為超越函式的情形)。特別地,當ν=1時,w(z)為亞純函式;當A(z)(j=0,1,…,ν)都為多項式時,w(z)為代數函式。
代數體函式首先由龐加萊(Poincaré,(J.-)H.)所引入,其後班勒衛(Painlevé,P.)、布特魯(Boutroux,P.L.)和馬爾姆奎斯特(Malmquist,J.)等人研究常微分方程時遇到此類函式。如同亞純函式一樣,代數體函式的主要研究內容之一是它的值分布理論。最早由雷蒙多斯(Rémoundos,G.)(1927)推廣了皮卡定理,他證明了ν值代數體函式至多有2ν個皮卡例外值,並指出存在具有2ν個皮卡例外值的代數體函式。其後瓦利隆(Valiron,G.)(1929)、烏利希(Ullricn,E.)(1931)和塞爾貝格(Selberg,A.)(1930-1934)分別用不同的方法對代數體函式建立了相當於亞純函式奈望林納理論的基本定理,即代數體函式的第一基本定理和第二基本定理。根據第二基本定理可以得到代數體函式的虧量關係以及重值和惟一性定理等重要結果。1933年,嘉當(Cartan,H.)討論了p(≥2)個全純函式的線性組合ag(z)+ag(z)+…+ag(z)的零點分布問題。特別地,當取a=a(j=1,2,…,p=ν+1)時,則相當於考慮ν值代數體函式的值分布。因此嘉當的討論能導出代數體函式的基本結果。
亞純函式
亞純函式是一類特殊的解析函式。指在z平面上除極點外無其他類型奇點的單值解析函式。如有理函式,tan z等。
除極點外為全純的函式為亞純函式,它是複變函數論研究的主要對象之一。
德國數學家外爾斯特拉斯、瑞典數學家米塔-列夫勒、法國數學家柯西等都是亞純函式理論的奠基人。1876年,外爾斯特拉斯證明了一個亞純函式可以表示為兩個整函式的商。第二年,瑞典數學家米塔-列夫勒推廣了外爾斯特拉斯的結果,證明在任意一個區域上的亞純函式皆可表示為兩個函式的商,其中每一個都在該區域內解析。法國數學家柯西也曾給出一種分解方法,對相當廣的一類亞純函式得到簡單的表示式。
近代亞純函式理論是20世紀20年代由芬蘭數學家奈望林納所創立。他在1925年發表了亞純函式的一個一般性理論,這個理論中有兩個基本定理分別被稱為第一基本定理和第二基本定理,從它們可以推出一系列關於亞純函式的值分布的結果,豐富並推進了前人的工作,產生了深遠影響。
亞純函式的術語是由法國數學家布里奧和布凱共同引進的。
代數函式
代數函式是一類完全解析函式。指由不可約方程:
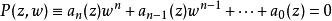 代數體函式
代數體函式確定的多值函式,其中a(z)(j=0,1,…,n)是z的多項式。從這個w的代數方程可知對每一個z值確定多個w值,因此w=w(z)是一多值函式。代數函式是在擴充的複平面C^上僅具有有限多個代數支點和極點的完全解析函式;反之,具有上述特徵的完全解析函式,必滿足一不可約代數方程,且除去一個非零常數因子外此方程是惟一的.相應於代數函式的黎曼曲面是緊緻的,即閉曲面。此曲面的虧格即定義為代數函式的虧格。由方程(1)聯繫著的z和w的有理函式R(z,w)之積分:
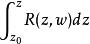 代數體函式
代數體函式稱為阿貝爾積分,其中w(z)的值是由z點選定的分支沿積分路徑解析開拓而得。它是一多值函式,其多值性不僅產生於R(z,w)的殘數,w(z)的多值性,而且還依賴於w(z)相應的黎曼曲面的拓撲性質。對於這個積分人們常尋找一系列標準形式,使得任一這類型的積分能通過適當的變數變換變為其中一個標準形式。
關於阿貝爾積分的研究導致代數函式的單值化問題,代數函式單值化又引起一般單值化理論的發展.在這方面,從19世紀下半期到20世紀的最初十年,世界上許多著名數學家如黎曼(Riemann,G.F.B.)、克萊因(Klein,(C.)F.)、龐加萊(Poincaré,J.-H.)、施瓦茲(Schwarz,H.A.)、諾伊曼(Neumann,C.G.)和克貝(Koebe,P.)等人都做出了重要貢獻。
重要人物
龐加萊
法國著名數學家、天文學家、物理學家和科學哲學家,1875年畢業於巴黎多科工藝學校,1879年以關於微分方程一般解的論文獲得博士學位,同年到卡昂大學任教,1881年入巴黎大學任教授,直到去世.他一生寫下了將近500篇科學論文和30部專著,這還不包括頗受歡迎的科學哲學著作和趣味盎然的科普著作。他的貢獻幾乎遍及了當時數學和物理學的全部領域。
龐加萊對數學的第一個重大貢獻是在1880年以後創立了自守函式理論,解決了解析函式的單值化問題。
1884年法國《數學學報》連續發表了他關於這一課題的5篇論文,立即使他獲得了世界性的聲譽.他又是多復變解析函式論的創始人,並在1883年的一篇短文中首先研究整函式的格與其泰勒展開的係數或者函式的絕對值的增長率之間的關係,成為整函式與亞純函式理論的開端。他最傑出的貢獻是創立了微分方程定性理論,他於1880—1886年發表的四篇大論文,使這一分支在一開始就發展到了幾乎完善的地步.1885年以後.他關於微分方程的論文都涉及天體力學,特別是三體問題,首創天體力學的嚴格處理方法,並因對三體問題的研究於1889年第一個獲得瑞典國王奧斯卡二世為“n體問題”設立的獎金.為了進一步研究線性微分方程,他對發散級數進行了深入討論,開創了漸近展開理論。在代數學中,他第一次引入了左理想與右理想的概念。1901年他的一篇數論論文成為有理數域(或代數數域)上的代數幾何學的開端.1901—1911年他關於代數曲面F(x,y,z)=0中所含的代數曲線的幾篇論文對代數幾何作出了突出貢獻.對代數拓撲學,他創造了單形的同調論的一整套方法,並由此引發了一系列重要結果.他又是數學基礎的直覺主義學派的先驅之一.此外,他對相對論和量子理論做出了具有啟發性的貢獻.他的科學哲學思想對20世紀眾多的科學家和哲學家產生了深遠的影響.他被譽為“理性科學的活躍智囊”,“本世紀初唯一留下的全才”,是對數學和它的套用具有全面知識的一個人。
班勒衛
法國數學家、政治家.生於巴黎,卒於巴黎.早年在巴黎大學和哥廷根大學學習,1887年獲博士學位.先後任教於巴黎理學院、巴黎綜合工科學校、法蘭西學院和巴黎高等師範學校.1900年當選為法國科學院院士.他曾獲得多項數學獎.
班勒衛的主要貢獻在代數曲線和代數曲面理論、微分方程的奇點理論等方面.他研究了代數曲線和代數曲面的有理變換問題,引入了雙一致變換.他成功地研究了代數微分方程的奇點理論,由形如y″=f(x,y,y′)的二階方程的解引出的新的超越函式,被稱為班勒衛超越函式.他還將其數學成果套用於分析力學,推廣了關於n體問題的結果,並修正了某些錯誤結論.
班勒衛對新興的航空技術頗感興趣,他是1908年雙翼飛機創紀錄飛行的一個乘客.他還熱心於政治活動,1910年被選為國民議會議員,其後還任公共教育部長、議長,1917年、1925年兩次當選為法國總理。
布特魯
法國數學家、歷史學家、科學哲學家。生於巴黎。父親是有名的哲學家。布特魯學於巴黎高等師範學校。1908—1920 年任普瓦蒂埃(Poitiers)大學積分學教授。先後在南錫(Nancy)大學、法蘭西學院和美國普林斯頓(Princeton)等大學任教。一次大戰中投入法國軍隊,1920年回到法蘭西學院,成為這裡的第一位科學史教授。布特魯在純數學方面的主要成就是關於多值函式和微分方程奇點問題的研究,在歷史學和科學哲學方面也做了許多開創性的工作。
嘉當
法國數學家。生於法國南錫,1923年入巴黎高等師範學校學習,1926年大學畢業,1928年獲博士學位.1929—1931年,任里爾大學講師;1931—1940年,任斯特拉斯堡大學教授;1940—1969年,任巴黎大學教授;1969—1975年,任南巴黎大學教授.1967—1970年,任國際數學聯盟主席.1965年,被選為法國科學院通訊院士,1974年成為院士.1971年,被選為倫敦皇家學會外籍會員,1972年,被選為美國全國科學院外籍院士。此外,他還是日本、波蘭、馬德里及北歐國家等近10家科學院、皇家科學院的院士或榮譽院士。
嘉當是法國布爾巴基學派的創始人之一。在複變函數、代數拓撲、位勢理論及同調代數等方面都做出了重要貢獻.他在複變函數論從單變數向多變數發展的過程中起了重要作用.他在20世紀30年代給出了全純自同構的惟一性定理、有界域全純自同構群的李群性質.1932年,他還證明了全純域與全純凸域的等價性的嘉當-蘇倫定理。他在1944年關於解析函式的理想的研究中得到的成果,同日本岡潔關於具有不定域的理想的研究,發展成了解析凝聚層理論.20世紀50年代初,他和塞爾(Serre,J.P.)在對施泰因流形的研究中引入了層係數的上同調理論,給出了多複變函數論中的嘉當定理,即施泰因流形上的凝聚解析層上的定理A和B.在第二次世界大戰後的15年內,他領導的著名的嘉當討論班,對代數拓撲的發展起了重要的促進作用。在討論班上引入的新方法,形成了同調代數的基礎.1954年,他和塞爾曾在上同調運算方面取得了重要成果.此外,他還引入了“濾子”等概念.他是法國第三級榮譽勛位的獲得者。1980年還獲沃爾夫數學獎.著作有《同調代數》(1956;與艾倫伯格(Eilenberg,S.)合著)等。他的主要論著均收入了三卷本的《嘉當文集》(1979)中。
