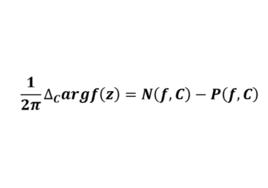對數留數
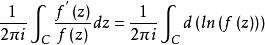 輻角原理
輻角原理 輻角原理
輻角原理積分 的值稱為複變函數 的對數留數。
 輻角原理
輻角原理設C是一條閉曲線,若 符合條件:
 輻角原理
輻角原理 輻角原理
輻角原理1) 在C內部除可能的極點外解析,即 為亞純函式;
 輻角原理
輻角原理2) 在C上解析且不為零,則有
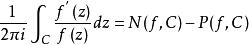 輻角原理
輻角原理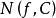 輻角原理
輻角原理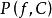 輻角原理
輻角原理 輻角原理
輻角原理其中 與 分別表示 在C的內部的零點和極點的個數(一個n級零點算作n個零點,而一個m級極點算作m個極點)。
定義
 輻角原理
輻角原理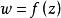 輻角原理
輻角原理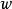 輻角原理
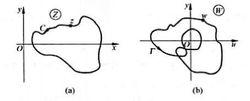
輻角原理設複變函數 ,當複平面Z上的z點沿閉曲線C的正向(逆時針)繞行一周時(如右圖a),複平面W上的 點就相應地畫出一條連續閉曲線Γ(如右圖b)。
根據複變函數對數的定義,有
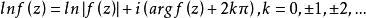 輻角原理
輻角原理由右圖以及上式可歸納出:
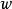 輻角原理
輻角原理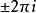 輻角原理
輻角原理1)當Γ是一條包含原點的簡單閉曲線時, 點沿Γ繞行一周,上式右端第1項的量沒有變化,而第2項的量改變了 (逆時針繞行取正,順時針取負);
2)當Γ曲線內不包含原點時,上式右端兩項的改變數均為零。
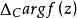 輻角原理
輻角原理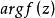 輻角原理
輻角原理設C是一條閉曲線,定義 為z沿著曲線C的正向繞行一周后 的改變數。
由此可得輻角原理如下:
 輻角原理
輻角原理 輻角原理
輻角原理設D是閉曲線C所圍成的區域,若(1) 在D內除可能的極點外解析,即為亞純函式;(2) 在C上解析且不為零,則
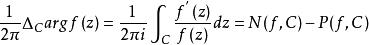 輻角原理
輻角原理證明
由牛頓-萊布尼茨公式可知:
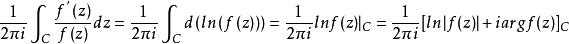 輻角原理
輻角原理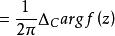 輻角原理
輻角原理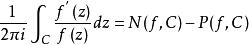 輻角原理
輻角原理再由
可知
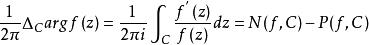 輻角原理
輻角原理得證。
套用
1)用於求解複變函數的零點或極點個數
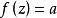 輻角原理
輻角原理2)用於求解方程的根的個數
3)在自動控制中,作為奈奎斯特穩定判據的理論基礎(奈奎斯特穩定判據用於分析單變數系統的穩定性)