定義
上不完全Γ函式和下不完全Γ函式的定義分別如下：
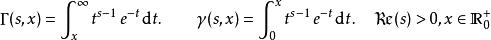不完全Γ函式通過解析延拓可以將定義域拓展到C×C（除去可數個奇點外），詳見下文。
記號
如無特別說明，在本文中，以x表示非負實數，以z表示任意複數。
基本性質
在上面定義的約束條件下，通過分部積分，可以計算得遞歸關係：
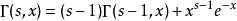不完全Γ函式以及反過來：
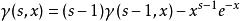不完全Γ函式
不完全Γ函式因為正常的 函式定義為：
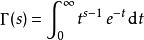不完全Γ函式故有：
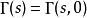不完全Γ函式
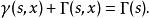不完全Γ函式以及
解析延拓
下不完全伽瑪函式
解析延拓的方法
在最原始的定義式中，積分是沿著實軸進行的，故要求在γ(s,z) 中，
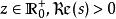不完全Γ函式運用上一小節裡面的關係式，可以用下式來進行解析延拓：
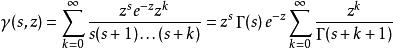不完全Γ函式由 比值審斂法可知，右邊的級數的收斂半徑是無窮大。
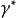不完全Γ函式由魏爾斯特拉斯原理，下式中的函式，有時記作 ，是關於s和z的整函式。
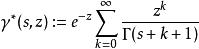不完全Γ函式因此下面的分解式
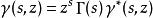不完全Γ函式的確給出了下不完全伽瑪函式的一個解析延拓。其中前兩個因子給出了下不完全伽瑪函式的奇點（即z=0 或s為非正整數），而後面的因子則給出了下不完全伽瑪函式的零點。
多值性
下不完全伽瑪函式的多值性來自於因子z的多值性。如無特別說明，本文限制z的輻角絕對值小於 π。
積分表達式
在選定了z的單值分支之後，下不完全伽瑪函式的積分定義式可以自然地拓展到z為任意複數的情形，只是此時該積分應該理解為複平面上的路徑積分，且積分路徑需避開單值分支間的割線。需注意的是此時仍然要求s的實部大於 0，否則積分不收斂。
z→∞ 時的極限
s為正實數的情形，有定義式有：
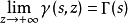不完全Γ函式s為複數且不為非正整數的情形，可以證明：
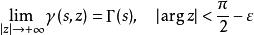不完全Γ函式後面的條件相當於要求z的實部為正值且輻角取主值。
總結
根據上面的討論，下不完全伽瑪函式有下列性質：
•當s為正整數時是z的整函式；
•當s不是整數時是z的多值全純函式，z=0 是其枝點；
•對於確定的z，指定主分支後，下不完全伽瑪函式是s的亞純函式，非正整數是其一階極點。
上不完全伽瑪函式
解析延拓的方法
當z為正實數，s為實部大於 0 的複數時，有定義顯然有：
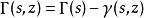不完全Γ函式由於伽瑪函式和下不完全伽瑪函式關於s,z都至少是亞純函式，上式可以自然地作解析延拓，並以此作為上不完全伽瑪函式的定義。下不完全伽瑪函式的多值性自然地導致上不完全伽瑪函式的多值性，下面的討論基於主分支。
進一步地，由黎曼可去奇點原理，由於等號右邊在s取非正整數時的鄰域內有界，故作為s的函式，非正整數是上不完全伽瑪函式的可去奇點，可以通過對等號右邊取極限來定義非正整數時上不完全伽瑪函式的值。下面以s=0 為例來說明這種極限過程，其它情況可以類推得到。
事實上，在下不完全伽瑪函式的積分表達式中，將指數函式用其泰勒展開式代換，得到：
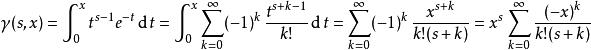不完全Γ函式即
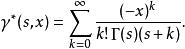不完全Γ函式上式實際上給出了γ(s,z) 的一個級數表示，給定s後，由比值審斂法知上式的收斂半徑為無窮大。下面的討論將x換成z（z≠0）。
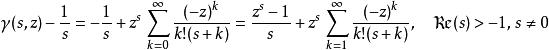不完全Γ函式上式等號右邊第二項當s=0 時有良好的定義，第一項在s→0 時的極限存在，故等號右邊於s→0 時的極限存在，並可以用它來定義等號左邊的值。
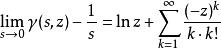不完全Γ函式另一方面，由伽瑪函式的魏爾斯特拉斯無窮乘積表示有：
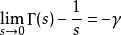不完全Γ函式γ是歐拉-馬歇羅尼常數。於是，可以定義
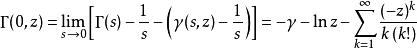不完全Γ函式這樣就證明了s=0 的確是上不完全伽瑪函式的可去奇點。
總結
上不完全伽瑪函式的其它解析性質可以由下不完全伽瑪函式和（完全）伽瑪函式的解析性質得到。結果如下：
•當s是正整數時，是z的整函式；
•當s不是整數時，是z的多值全純函式，z=0 是其枝點；
•選定單值分支後，對z≠0，是s的整函式；
•當s的實部大於零且z=0 時，等於（完全）伽瑪函式 Γ(s)；
注意最後一條對一般的s並不成立。特別地，當s為負實數且不為整數時，Γ(s) 是實數，而 Γ(s,0) 沒有定義。
特殊值
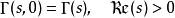不完全Γ函式下面一組關係式都能夠由積分表達式直接得出，其中第三、四式中的函式是指數積分，第五、六式中的函式分別是余誤差函式和誤差函式：
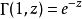不完全Γ函式
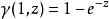不完全Γ函式
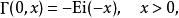不完全Γ函式
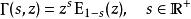不完全Γ函式
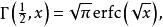不完全Γ函式
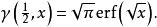不完全Γ函式導函式
由不完全伽瑪函式的積分表達式顯然有：
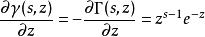不完全Γ函式儘管積分表達式為保證收斂性要加上s的實部大於零的限制，但上式並沒有這種限制。這可以通過s的實部大於零時的對應表達式兩邊作解析延拓證明。
另一方面，不完全伽瑪函式對s的偏導數是MeijerG-函式的特例，事實上，定義
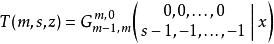不完全Γ函式則有：
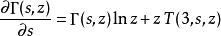不完全Γ函式
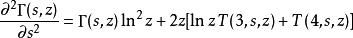不完全Γ函式更一般地：
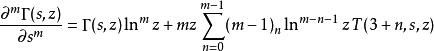不完全Γ函式式中 (m-1)是下降階乘冪的 Pochhammer 記號。
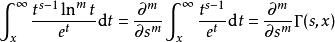不完全Γ函式事實上
利用上式和Mellin 變換的性質，並作解析延拓，就可以得到上不完全伽瑪函式對參變數的高階偏導數的表達式。
