公式簡介
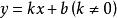線段中垂線解析式公式
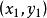線段中垂線解析式公式
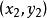線段中垂線解析式公式若有線段（一端坐標為,另一端坐標為），則其中垂線（垂直平分線）的函式解析式為：
線段中垂線解析式公式證明
題目：給定一線段y=kx+b（一端坐標為(x1,y1),另一端坐標為（x2,y2)）,求其垂直平分線的函式解析式
設其中垂線為 f=k1x+c
∵f⊥y
∴k1*k=-1,即k1=-1/k
∴f=-1/k*x+c,即f=-x/k+c;
把點（(x1+x2)/2,(y1+y2)/2）代入f=-x/k+c中
得(y1+y2)/2=-((x1+x2)/2)/k+c
化簡得c=(y1+y2)/2+(x1+x2)/2k
∴f=-x/k+c代入即可得
f=-x/k+(x1+x2)/2k+(y1+y2)/2
例子
例如：設線段AB的中點為C,則AB的垂直平分線L過點C.
設 A(x1,y1) B(x2,y2）,則中點C的坐標為{(x1+x2)/2,(y1+y2)/2)}
由AB的斜率k=(y2-y1)/(x2-x1) 可得AB的垂直平分線L的斜率為:-1/k
根據點斜式可求出
AB 垂直平分線L：y=-(x2-x1)/(y2-y1)* [x-(x1+x2)/2]+(y1+y2)/2
套用
1、已知一次函式y=3x-1 的圖像經過點A(a，b)和點B(a+1,b+k)。
①求k的值。
②若A點在y軸上，求B點的坐標。
③在②的條件下，說明在x軸上是否存在點P使得△BOP為等腰三角形？若存在，直接寫出P點的坐標；若不存在，請說明理由。
解(只為了運用中垂線解析式公式，故直接1、2兩小題直接寫答案)：
①k=3
②B（1,2）
③P1（2,0）P2（√5,0）P3（-√5,0）
P4（作中垂線交x軸的點）：(2.5,0) 由於B（1,2），O（0,0）所以線段OB ：y=2x;
則它的中垂線解析式為 y=-x/2+1/4+1合 y=-x/2+1.25；
則與x軸交點為（2.5，0）；
