定義
 賦范空間
賦范空間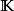 賦范空間
賦范空間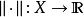 賦范空間
賦范空間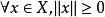 賦范空間
賦范空間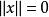 賦范空間
賦范空間 賦范空間
賦范空間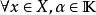 賦范空間
賦范空間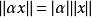 賦范空間
賦范空間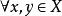 賦范空間
賦范空間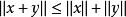 賦范空間
賦范空間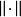 賦范空間
賦范空間 賦范空間
賦范空間 賦范空間
賦范空間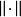 賦范空間
賦范空間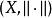 賦范空間
賦范空間 賦范空間
賦范空間向量的範數是長度概念的推廣。設
是域(實數域或複數域)上的線性空間,函式滿足條件:1)對;且若且唯若;
2)對,有(齊次性);
3)對,有(三角不等式)。
稱是上的一個範數,上定義了範數稱為(線性)賦范空間,記為,有時簡記為。
範數誘導的距離
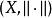 賦范空間
賦范空間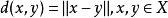 賦范空間
賦范空間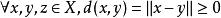 賦范空間
賦范空間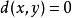 賦范空間
賦范空間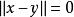 賦范空間
賦范空間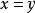 賦范空間
賦范空間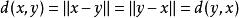 賦范空間
賦范空間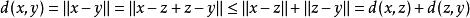 賦范空間
賦范空間在一個賦范空間
中,通過範數可以自然地定義一個距離,。
事實上,由範數公理,對,且,若且唯若,即;
;
。
稱賦范空間中這個距離是由範數誘導的距離。
強(或按范)收斂
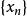 賦范空間
賦范空間 賦范空間
賦范空間 賦范空間
賦范空間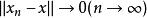 賦范空間
賦范空間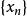 賦范空間
賦范空間 賦范空間
賦范空間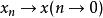 賦范空間
賦范空間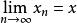 賦范空間
賦范空間設
是賦范空間中的點列,,如果,
稱強(或按范)收斂於,記為
,
或
。
Banach空間
如果賦范空間按強收斂是完備的,就稱它為 Banach空間。
性質
性質1
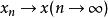 賦范空間
賦范空間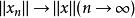 賦范空間
賦范空間範數是一個連續函式,即當時,。
性質2
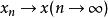 賦范空間
賦范空間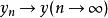 賦范空間
賦范空間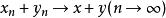 賦范空間
賦范空間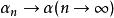 賦范空間
賦范空間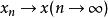 賦范空間
賦范空間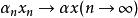 賦范空間
賦范空間線性運算是連續的,即當
及時,;當及時,。
性質3
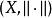 賦范空間
賦范空間 賦范空間
賦范空間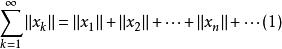 賦范空間
賦范空間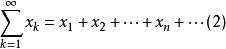 賦范空間
賦范空間設
是賦范空間。如果是完備的且級數收斂,則級數
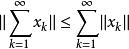 賦范空間
賦范空間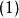 賦范空間
賦范空間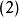 賦范空間
賦范空間收斂且
。反之,如果在一個賦范空間中,任意無窮級數收斂必有級數收斂,則空間是Banach空間。
拓撲結構
如果(V,‖·‖)是規範向量空間,則‖·‖引入度量(距離的概念),並因此導致V上的拓撲。該度量以自然的方式定義:兩個向量之間的距離u v由||u-v||給出。這種拓撲正是最弱的拓撲結構,使得“‖”連續,並且與以下意義上的V的線性結構兼容:
向量加法+:V×V→V相對於該拓撲結合是連續的。這直接來自三角不等式。
標量乘法:K×V→V,其中K是V的底層標量場,是聯合連續的。這取決於三角不平等和規範的均勻性。
類似地,對於任何半規範向量空間,我們可以將兩個向量u和v之間的距離定義為‖u-v‖。這將把這個空間變成一個假的空間(注意這比一個度量要弱),並允許定義諸如連續性和收斂的概念。為了更抽象地說,每個半規範向量空間是一個拓撲向量空間,因此承載了由半規範引起的拓撲結構。
特別感興趣的是稱為Banach空間的完整規範空間。每個規範向量空間V坐在Banach空間內的一個密集子空間;這個Banach空間本質上是由V定義的,稱為V的完成。
有限維向量空間上的所有規範從拓撲觀點是相等的,因為它們誘導相同的拓撲(儘管所得的度量空間不必相同)。並且,由於任何歐幾里德空間是完整的,因此我們可以得出結論,所有有限維的規範向量空間是Banach空間。若且唯若單位球B = {x:‖x‖≤1}緊湊時,規範向量空間V是局部緊湊的,若且唯若V是有限維的情況下才是這種情況;這是雷斯的引理的結果。 (事實上,更一般的結果是真實的:若且唯若它是有限維度時,拓撲向量空間是局部緊湊的,這裡的意思是我們不假定拓撲來自一個規範。
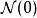 賦范空間
賦范空間信號向量空間的拓撲具有許多不錯的屬性。給定一個約0的鄰域系統,我們可以構建所有其他鄰域系統:
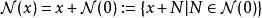 賦范空間
賦范空間與:
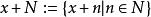 賦范空間
賦范空間此外,存在由吸收和凸集組成的0的鄰域基礎。由於該屬性在功能分析中非常有用,因此在名稱為局部凸空間的情況下研究了具有該屬性的規範向量空間的泛化。
