一般
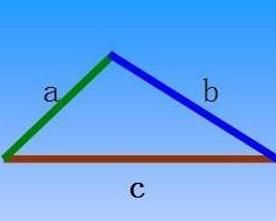
設三角形三邊為a,b,c則
a+b>c,a>c-b
b+c>a,b>a-c
a+c>b,c>b-a
三角形三邊關係如圖，
任意△ABC，求證AB+AC>BC。
證明：在BA的延長線上取AD=AC
則∠D=∠ACD（等邊對等角）
∵∠BCD>∠ACD
∴∠BCD>∠D
∴BD>BC（大角對大邊）
∵BD=AB+AD=AB+AC
∴AB+AC>BC
基本定理
在一個三角形中，任意兩邊之和大於第三邊，任意兩邊之差小於第三邊。
設三角形三邊為a,b,c則
a+b>c
a+c>b
b+c>a
a-b
a-c
b-c
在直角三角形中，設a、b為直角邊，c為斜邊。
則兩直角邊的平方和等於斜邊平方。（勾股定理）
在等邊三角形中，a=b=c
在等腰三角形中，若a,b為兩腰，則a=b
在三角形ABC的內角A、B、C所對邊分別為a、b、c的情況下，c^2=a^2+b^2-2abcosc
特殊
直角三角形
性質1：直角三角形兩直角邊的平方和等於斜邊的平方。 性質2：在直角三角形中，兩個銳角互余。 性質3：在直角三角形中，斜邊上的中線等於斜邊的一半。
性質4：直角三角形的兩直角邊的乘積等於斜邊與斜邊上高的乘積。性質5:如圖，Rt△ABC中，∠BAC=90°，AD是斜邊BC上的高，則有射影定理如下：
（1） AD^2=BD·DC，
（2） AB^2=BD·BC ， 射影定理圖
（3） AC^2=CD·BC 。 等積式 （4）ABXAC=ADXBC (可用面積來證明） (5)直角三角形的外接圓的半徑R=1/2BC,
(6)直角三角形的內切圓的半徑r=1/2(AB+AC-BC)(公式一)；r=AB*AC/(AB+BC+CA)(公式二)
三角形三邊關係等腰直角三角形三邊之比：1:1:根號二
