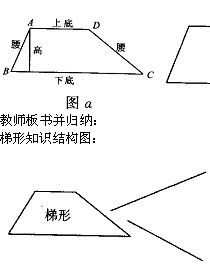
概念
梯形(trapezium)是指一組對邊平行而另一組對邊不平行的四邊形。平行的兩邊叫做梯形的底邊,其中長邊叫下底,短邊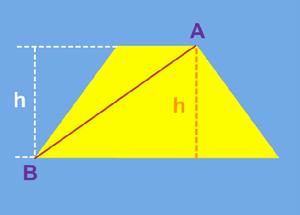 梯形
梯形分類
一腰垂直於底的梯形叫直角梯形,
兩腰相等的梯形叫等腰梯形。
等腰梯形的性質
1.等腰梯形的兩條腰相等
2.等腰梯形在同一底上的兩個底角相等
3.等腰梯形的兩條對角線相等
4.等腰梯形是軸對稱圖形,對稱軸是上下底中點的連線所在直線
5.等腰梯形(這個非等腰梯形同理)的中位線(兩腰中點相連的線叫做中位線)等於上下底和的二分之一注意:在有些情況下,梯形的上下底以長短區分,而不是按位置確定的,把較短的底叫做上底,較長的底叫做下底。
判定
1.一組對邊平行,另一組對邊不平行的四邊形是梯形(一組對邊平行且不相等的四邊形是梯形)
2.兩腰相等的梯形是等腰梯形
3.同一底上的兩個角相等的梯形是等腰梯形
4.有一個內角是直角的梯形是直角梯形
5.對角線相等的梯形是等腰梯形.
6.梯形的中位線等於上底加下底和的一半,且平行於上底和下底。
 梯形
梯形周長、面積
梯形的面積公式
:(上底+下底)×高÷2。
等腰梯形面積公式
:中位線×高用字母表示:(a+b)×h÷2 或l·h周長
梯形的周長公式
:上底+下底+腰+腰用字母表示:a+b+c+d
等腰梯形的周長公式
:上底+下底+2腰用字母表示:a+b+2c
對角線互相垂直的梯形
:對角線×對角線÷2
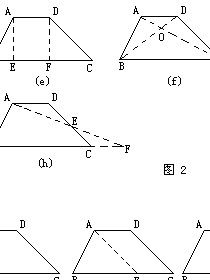
、如圖(6),在等腰梯形ABCD中,AD∥BC,AB=DC,且AC⊥BD,AF是梯形的高,梯形的面積是49cm2.求梯形的高。
解法1:如圖(甲),過A作AE∥DB交CB的延長線於點E。
∵AC⊥BD,
圖(6)∴AC⊥AE.
∵AD∥EB,
∴AE=BD,EB=AD.
又∵四邊形ABCD是等腰梯形,
 梯形
梯形∴AC=BD.
∴AE=AC.
∴△AEC是等腰直角三角形.
又AF是斜邊上的高,故AF也為斜邊上的中線.
∴AF=7cm
解法2: 設梯形ABCD的兩條對角線相交於O點,過O作OH⊥BC於點H,延長HO交AD於G點(如圖(乙)).
∵AD∥BC,
∴HG⊥AD.
∵AB=DC,AC=DB,BC公共,
∴△ABC≌△DCB.
∴∠2=∠1.
又∵AC⊥BD,
∴△BOC是等腰直角三角形.
∴同理.
∴以下解答過程與解法1相同.
解法3:過D作DM⊥BC於點M(如圖(丙)).
∵梯形ABCD是等腰梯形,
∴AC=DB,∠ABC=∠DCB.
又∵AF=DM,
∴Rt△AFC≌Rt△DMB,
∴∠DBC=∠ACB.
又∵AC⊥BD,
∴∠DBM=∠ACF=45°.
∴△AFC和△DMB都是等腰直角三角形.AF=FC,DM=MB,
∴. 以下解答過程與解法1相同.
點評: 本題的三種解法都是利用等腰直角三角形的性質或全等三角形的性質來證明該梯形的高就等於該梯形的中位線的長.因此,在等腰梯形中,若兩條對角線垂直,則這個梯形的高就等於中位線的長,梯形的面積就等於高的平方.
如圖(7),在梯形ABCD中,AD//BC,AB=DC,點E,F,G分別在邊AB,BC,CD上,且AE=GF=GC.
(1)求證四邊形AEFG是平行四邊形;
(2)當∠FGC=2∠EFB時,求證四邊形AEFG是矩形.
分析:本題考查有關三角形、四邊形的綜合證明.涉及到等腰梯形的性質、平行四邊形的判定與性質、等腰三角形的性質等.在解答過程中要注意證明格式、推理方式的規範化.
證明:(1)∵在梯形ABCD中,AB=DC,
∴∠B=∠C.
∵GF=GC,∴∠C=∠GFC,
∴∠B=∠GFC
∴AB//GF,即AE//GF.
又∵AE=GF
∴四邊形AEFG是平行四邊形.圖(7)
(2)解:過點G作GH⊥FC,垂足為H.
∵GF=GC,
∴∠FGH=1/2∠FGC.
∵∠FGC=2∠EFB
∴∠FGH=∠EFB.
∵∠FGH+∠GFH=90°
∴∠EFB+∠GFH=90°
∴∠EFG=90°
∵四邊形AEFG是平行四邊形,
∴四邊形AEFG是矩形.
備註
:梯形的底角可以指梯形中任意一個角,所以說“底角相等的梯形是等腰梯形”是不對的。