性質
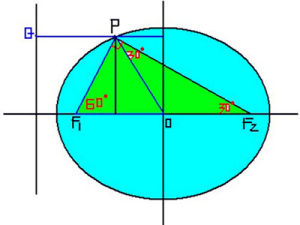
已知橢圓方程為x2a2+y2b2=1(ab0)兩焦點分別為F1,F2,設焦點三角形PF1F2中∠F1PF2=θ,則S(1)|PF1|+|PF2|=2a
(2)4c²=|PF1|²+|PF2|²-2|PF1|·|PF2|·cosθ
(3)周長2a+2c
證明
公式
 橢圓焦點三角形
橢圓焦點三角形角F2F1P=α,F1F2P=β,F1PF2=θ,
則有離心率e=sin(α+β)/(sinα+sinβ),
焦點三角形面積S=b^2*(tan(θ/2))。
方法
設F1P=m,F2P=n,2a=m+n,
由射影定理得2c=mcosβ+ncosα,
e=c/a=2c/2a=mcosβ+ncosα/(m+n),
由正弦定理e=sinαcosβ+sinβcosα/(sinβ+sinα)=sin(α+β)/(sinα+sinβ)。
對於焦點△F1PF2,設PF1=m,PF2=n
則m+n=2a
在△F1PF2中,由餘弦定理:
(F1F2)^2=m^2+n^2-2mncosθ
即4*c^2=(m+n)^2-2mn-2mncosθ=4a^2-2mn(1+cosθ)
所以mn(1+cosθ)=2a^2-2c^2=2b^2
所以mn=2b^2/(1+cosθ)
S=(mnsinθ)/2.............(正弦定理的三角形面積公式)
=b^2*sinθ/(1+cosθ)
=b^2*[2sin(θ/2)cos(θ/2)]/2[cos(θ/2)]^2
=b^2*sin(θ/2)/cos(θ/2)
=b^2*(tan(θ/2))
例題
F1,F2是橢圓x^2/a^2+y^2/b^2=1(a>b>0)的焦點,PQ是過F1的一條弦,求三角形PQF2面積的最大值
【解】
S△PQF2=S△QF1F2+S△QF1F2=1/2*|y2-y1|*2c=c*|y2-y1|
△QF1F2與△QF1F2底邊均為F1F2=2c,之後是聯立直線方程與橢圓方程,利用韋達定理表示出|y2-y1|進行分析即可
【|y1-y2|=√(1+1/k^2)[(y1+y2)^2-4y1y2]】
請你看下面的一個具體例題,會對你有所啟發的。
設點F1是x^2/3+y^2/2=1的左焦點,弦AB過橢圓的右焦點,求三角形F1AB的面積的最大值。
【解】a^2=3,b^2=2,c^2=3-2=1→→c=1∴F1F2=2c=2
假設A在x上方,B在下方直線過(1,0)
設直線是x-1=m(y-0)x=my+1
代入2x^2+3y^2=6(2m^2+3)y^2+4my-4=0→→y1+y2=-4m/(2m^2+3),y1y2=-4/(2m^2+3)
△F1AB=△F1F2A+△F1F2B他們底邊都是F1F2=2則面積和最小就是高的和最小(即|y1|+|y2|最小)
∵AB在x軸兩側,∴一正一負→→|y1|+|y2|=|y1-y2|(y1-y2)^2=(y1+y2)^2-4y1y2=16m^2/(2m^2+3)2+16/(2m^2+3)→→|y1-y2|=4√[m2+(2m2+3)]/(2m2+3)=4√3*√(m2+1)]/(2m2+3)
令√(m^2+1)=p2m^2+3=2p^2+1且p>=1則p/(2p^2+1)=1/(2p+1/p)(分母是對勾函式)
∴p=√(1/2)=√2/2時最小這裡p>=1→→p=1,2p+1/p最小=3
此時p/(2p2+1)最大=1/3→→|y1-y2|最大=4√3*1/3∴最大值=2*4√3/3÷2=4√3/3
在橢圓中,我們通常把焦點與過另一個焦點的弦所圍成的三角形叫做焦點三角形,類似地,我們也把頂點與過另一個頂點所對應的焦點弦圍成的三角形叫頂焦點三角形。
在橢圓的頂焦點三角形中有許多與橢圓焦點三角形相類似的幾何特徵,蘊涵著橢圓很多幾何性質,在全國各地的聯考模擬試卷及聯考試題中,都曾出現過以“頂焦點三角形”為載體的問題.本文對橢圓的頂焦點三角形的性質加以歸納與剖析.