三角形中線定理

中線定理（pappus定理），又稱阿波羅尼奧斯定理，是歐氏幾何的定理，表述三角形三邊和中線長度關係。表達式為AB²+AC²=2(BI²+AI²)。

基本信息

• 中文名：三角形中線定理
• 英文名：pappus定理

• 別稱：阿波羅尼奧斯定理
• 表達式：AB²+AC²=2(BI²+AI²)
• 提出者：阿波羅尼奧斯
• 學科：數學幾何
• 適用領域範圍：三角

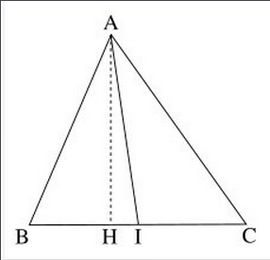
中線定義

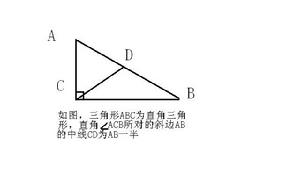三角形中線定理

三角形中，連線一個頂點和它所對邊的中點的線段叫做三角形的中線。

任何三角形都有三條 中線，而且這三條中線都在三角形的內部，並交於一點

由定義可知，三角形的 中線是一條線段。

由於三角形有三條邊，所以一個三角形有三條中線。

且三條 中線交於一點。這點稱為三角形的重心。

每條 三角形中線分得的兩個三角形面積相等。

性質

三角形中線定理

設⊿ABC的角A、B、C的對邊分別為a、b、c．
1、三角形的三條中線都在三角形內。
2、三角形的三條中線長：
................______________
ma=(1/2)√2b²+2c²-a²；
................______________
mb=(1/2)√2c²+2a²-b²；
................______________
mc=(1/2)√2a²+2b²-c²。
(ma,mb,mc分別為角A,B,C所對的中線長）
3、三角形的三條中線交於一點，該點叫做三角形的重心。
4、直角三角形斜邊上的中線等於斜邊的一半。
5.三角形中線組成的三角形面積等於這個三角形面積的3/4.

中線定理

中線定理（pappus定理），又稱阿波羅尼奧斯定理，是歐氏幾何的定理，表述三角形三邊和中線長度關係。
定理內容：三角形一條中線兩側所對邊平方和等於底邊的一半平方與該邊中線平方和的2倍。
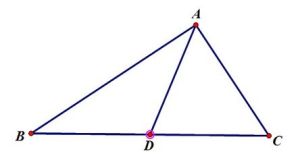
即，對任意三角形△ABC，設I是線段BC的中點，AI為中線，則有如下關係：
AB²+AC²=2(BI²+AI²)
或作AB²+AC²=1/2（BC）²+2AI²

定理證明

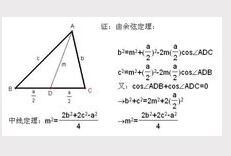三角形中線定理

除圖示給出的方法外，c1c2clone在此給出另外的兩種常規證明方法：

第一種是以中點為原點，在水平和豎直方向建立坐標系，

設：A(m,n),B(-a,0),C(a,0)，

則：(AD)²+(CD)²=m²+n²+a²

(AB)²+(AC)²=(m+a)²+n²+(m-a)²+n²=2(m²+a²+n²)

∴(AB)²+(AC)²=2[(AD)²+(CD)²]

第二種是在不同三角形中，對同一個角用兩次餘弦定理，比如對圖示中的∠B（或者∠C）在△ABD和△ABC（或者△ACD和△ABC）使用餘弦定理，從而直接得到三角形邊長的關係，進而得證。