歷史
勒貝格在1901年描述勒他的測度,隨後在第二年他描述了勒貝格積分。二者都是作為他在1902年的博士論文的一部分發表的。
例子
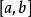 勒貝格測度
勒貝格測度 勒貝格測度
勒貝格測度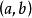 勒貝格測度
勒貝格測度1.如果A是一個區間 , 那么其勒貝格測度是區間長度 。開區間 的長度與閉區間一樣,因為兩集合的差是零測集。
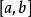 勒貝格測度
勒貝格測度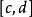 勒貝格測度
勒貝格測度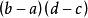 勒貝格測度
勒貝格測度2. 如果A是區間 和 的笛卡爾積,則它是一個長方形,測度為它的面積 。
3.康托爾集是一個 勒貝格測度為零的不可數集的例子。
性質
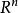 勒貝格測度
勒貝格測度上的勒貝格測度有如下的性質:
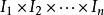 勒貝格測度
勒貝格測度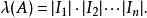 勒貝格測度
勒貝格測度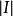 勒貝格測度
勒貝格測度1. 如果A是區間 的笛卡爾積,那么A是勒貝格可測的,並且 其中 表示區間I的長度。
2. 如果A是有限個或可數個兩兩互不相交的勒貝格可測集的並,那么A也是勒貝格可測的,並且λ(A) 就是這些可測集的測度的和(或無窮級數的和)。
3. 如果A勒貝格可測的,那么它的補集(相對於 R)也是可測的。
4. 對於每個勒貝格可測集A,λ(A) ≥ 0。
5. 如果A與B是勒貝格可測的,且A是B的子集,那么λ(A) ≤ λ(B)。 (由 2, 3 及 4可得。)
6. 可數多個是勒貝格可測集的交或者並仍然是勒貝格可測的。 (由2,3 可得)。
7. 如果A是一個開集或閉集,且是 R(甚至Borel集,見度量空間,待補)的子集,那么A是勒貝格可測的。
8. 如果A是一個勒貝格可測集,並有 λ(A) = 0 (零測集),則A的任何一個子集也是零測集。
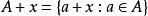 勒貝格測度
勒貝格測度9. 如果A是勒貝格可測的,x是 R中的一個元素,A關於x的平移(定義為 )也是勒貝格可測的,並且測度等於A.
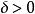 勒貝格測度
勒貝格測度 勒貝格測度
勒貝格測度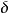 勒貝格測度
勒貝格測度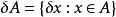 勒貝格測度
勒貝格測度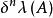 勒貝格測度
勒貝格測度10. 如果A是勒貝格可測的, ,則 關於 的擴張(定義為 )也是勒貝格可測的,其測度為 。
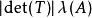 勒貝格測度
勒貝格測度11. 更廣泛地說,設T是一個線性變換,A是一個 R的勒貝格可測子集,則T(A)也是勒貝格可測的,其測度為 。
12. 如果A是R的勒貝格可測子集,f是一個A到R上的連續單射函式,則f(A)也是勒貝格可測的。
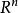 勒貝格測度
勒貝格測度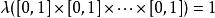 勒貝格測度
勒貝格測度簡要地說, 的勒貝格可測子集組成一個含所有區間及其笛卡爾積的σ代數,且λ是其上唯一的完備的、平移不變的、滿足 的測度。
勒貝格測度是 σ-有限測度。
零測集
 勒貝格測度
勒貝格測度的子集是零測集,如果對於每一個ε > 0,它都可以用可數個n個區間的乘積來覆蓋,其總體積最多為ε。所有可數集都是零測集。
 勒貝格測度
勒貝格測度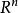 勒貝格測度
勒貝格測度如果 的子集的豪斯多夫維數小於n,那么它就是關於n維勒貝格測度的零測集。在這裡,豪斯多夫維數是相對於 上的歐幾里得度量(或任何與其等價的利普希茨度量)。另一方面,一個集合可能拓撲維數小於n,但具有正的n維勒貝格測度。一個例子是史密斯-沃爾泰拉-康托爾集,它的拓撲維數為0,但1維勒貝格測度為正數。
為了證明某個給定的集合A是勒貝格可測的,我們通常嘗試尋找一個“較好”的集合B,與A只相差一個零測集,然後證明B可以用開集或閉集的可數交集和並集生成。
勒貝格測度的結構
勒貝格測度的現代結構,基於外測度,是卡拉特奧多里發明的。
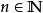 勒貝格測度
勒貝格測度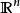 勒貝格測度
勒貝格測度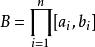 勒貝格測度
勒貝格測度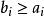 勒貝格測度
勒貝格測度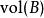 勒貝格測度
勒貝格測度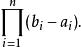 勒貝格測度
勒貝格測度固定 , 中的 盒子是形如 的集合,其中 。這個盒子的體積 定義為
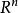 勒貝格測度
勒貝格測度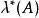 勒貝格測度
勒貝格測度對於任何 的子集A,我們可以定義它的外測度 :
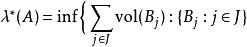 勒貝格測度
勒貝格測度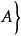 勒貝格測度
勒貝格測度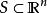 勒貝格測度
勒貝格測度是可數個盒子的集合,它的並集覆蓋了 。然後定義集合A為勒貝格可測的,如果對於所有集合 ,都有:
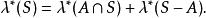 勒貝格測度
勒貝格測度這些勒貝格可測的集合形成了一個σ代數。勒貝格測度定義為λ(A) = λ(A)對於任何勒貝格可測的集合A。
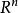 勒貝格測度
勒貝格測度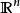 勒貝格測度
勒貝格測度根據維塔利定理,存在實數 的一個勒貝格不可測的子集。如果A是 的任何測度為正數的子集,那么A便有勒貝格不可測的子集。
與其他測度的關係
在所定義的集合上,博雷爾測度與勒貝格測度是一致的;然而,仍然有更多勒貝格可測的集合不是博雷爾可測的。博雷爾測度是平移不變的,但不是完備的。
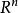 勒貝格測度
勒貝格測度哈爾測度可以定義在任何局部緊群上,是勒貝格測度的一個推廣(帶有加法的 是一個局部緊群)。
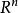 勒貝格測度
勒貝格測度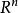 勒貝格測度
勒貝格測度豪斯多夫測度(參見豪斯多夫維數)是勒貝格測度的一個推廣,對於測量 的維數比n低的子集是很有用的,例如 內的曲線或曲面,以及分形集合。不能把豪斯多夫測度與豪斯多夫維數的概念混淆。
可以證明,在無窮維空間不存在勒貝格測度的類似物。
