譜論
正文
泛函分析中研究運算元的譜的理論。運算元的譜的概念是有限維矩陣的特徵值概念的推廣。力學、物理和工程技術中的大量問題在一定的條件下可以歸結為數學上代數方程、微分方程、積分方程或微分積分方程等的求解問題。在對這些方程求解問題的研究獲得豐富成果的基礎上，逐漸形成了一般的運算元的譜的理論（這裡主要指線性運算元）。數學上各類線性方程的求解問題可以概括為某個拓撲線性空間X上的方程(λI-T)x=y的求解,這裡T是X上已知的線性運算元，I為X的單位運算元，
λ是一個復參數。當X是有限維空間（例如維數為n）時，T可表示為一個n階方陣,而上面的方程就是n階線性方程組。線上性代數中，已經完全解決了它的求解問題,主要結果有:上述方程對一切y∈X有解若且唯若λ不是T的特徵值,而且這時解有惟一的形式x=(λI-T)-1y。對λ是T的特徵值的情況，也給出 y應滿足什麼條件才能使上述方程有解和解的一般表達式。當X是無限維空間時,問題變得複雜多了。1900～1903年，（E.）I.弗雷德霍姆研究了具有連續核的積分方程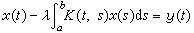
,得到了與有限維空間情形相類似的結果。後來,F.（F.）里斯、J.P.紹德爾建立了巴拿赫全連續運算元的弗雷德霍姆理論。1904～1906年D.希爾伯特考察了具有對稱核(即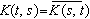
)的積分方程，後來又有了一般的有界自共軛運算元的譜理論。20年代J.馮·諾伊曼為適應量子力學的需要，發展了希爾伯特空間上（無界）自共軛運算元的譜理論並得到了酉運算元和正常運算元的譜分解定理。由於各種非交換的關係研究需要，40年代以後對希爾伯特空間上各種非正常運算元的研究也陸續開始，並取得了豐富的成果，已成為現代線性運算元譜論的重要方面。另一方面，關於巴拿赫空間上運算元的譜論,自從1913年F.里斯的研究以來,也取得了一系列的成果（見譜運算元）。 預解集和譜 巴拿赫空間上線性運算元譜點的概念是有限維矩陣特徵值概念的推廣。設T是巴拿赫空間，X到X的線性運算元,定義域為D(T),
λ為複數。如果(λI-T)有定義在全空間X上的有界的逆運算元，那么稱λ是運算元T的正則點。T的正則點全體稱為T的預解集,記為ρ(T)。ρ(T)的余集C \ρ(T)稱為T的譜集,簡稱為譜,記為σ(T)。因此 σ(T)是由那些使 (λI－T)沒有定義在全空間上的有界的逆運算元的複數λ全體組成。σ(T)中的複數稱為T的譜點。T的譜點有以下幾類:①(λI-T)沒有逆運算元,這時X中必存在x≠0，使(λI-T)x=0,稱這種λ為T的點譜(或特徵值)，其全體記為σp(T)。②(λI－T)沒有有界的逆運算元，這時必存在xn∈X,‖xn‖=1使‖(λI-T)xn‖→0，稱這種λ為T的近似點譜,其全體記為σα(T)。③(λI-T)有有界逆運算元,但不定義於全空間,稱這種λ為T的剩餘譜,其全體記為σr(T)。④(λI-T)有稠定逆運算元,而逆運算元是無界的，稱這種λ為T的連續譜，其全體記為σ0(T)。 當T是巴拿赫空間X上稠定閉運算元時，ρ(T)必是複平面上開集，從而σ(T)是閉集，(λI-T)-1是定義在ρ(T)上的運算元值解析函式,稱為T的預解式,常記為R(λ ,T)。在點λ 0∈ρ(T)的附近R(λ，T)必有展開式
，
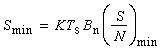λ,μ∈ρ(T)，成立預解式方程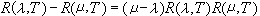 
。
∈σ(T)} 為 T的譜半徑，且有著名的譜半徑公式：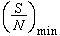
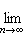
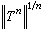。如果r(T)=0,那么稱T是廣義冪零運算元。冪零運算元T(即存在自然數k，使Tk=0)必是廣義冪零運算元。對希爾伯特空間上正常運算元N，有r(N)=‖N‖。 譜測度 設(
,B)是一個可測空間,B是一個σ代數(見測度論)，E是定義在 B上取值為希爾伯特空間h上投影運算元的映射；如果滿足①E()=I,②可列可加性(若{Mn}是B中一列互不相交的集合,則成立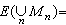
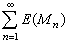，那么稱E為(,B)上譜測度，(,B,E)為h上的譜測度空間。 設(
,B,E)是h上一個譜測度空間,ƒ是(,B)上可測函式。如果存在h上運算元F，使對一切x，y∈h成立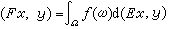
(也記作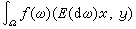
，上式右邊表示ƒ關於由
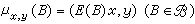定義的複測度
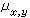的積分）,就稱F是ƒ關於E的譜積分，記為
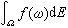或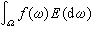
。 譜測度的支集 設
是n維歐幾里得空間Rn,B是Rn上波萊爾集全體,(Rn,B,E)是希爾伯特空間h上譜測度空間。如果有Rn中開集G,使得E(G)=0,則必有按集的包含關係為最大的開集G0,使得E(G0)＝0。稱閉集σ=Rn-G0為E的支集，記為 suppE，換言之，σ是滿足E(s)＝I中（按包含關係為）最大的閉集,形象地說即譜測度E集中在閉集suppE上，並且 E不能集中在比suppE更小的閉集上，易知譜積分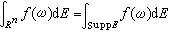
。 對於
是拓撲空間，B是上波萊爾集或貝爾集全體，在適當假設下就能將譜測度支集的概念推廣到(,B,E)的情況。 譜系 類似於單調增加右連續的（點）函式與勒貝格-斯蒂爾傑斯測度（集函式）的關係,對於譜測度（集的投影運算元值函式）與“單調增加右連續的”（點）投影運算元值函式也存在。下面以
=R1（實直線）為例:設(R1,B, E)是希爾伯特空間h上的譜測度空間,規定Eλ=E((-∞,λ】)，(λ∈(-∞，∞)),這時函式Eλ滿足①單調性，當λ≥μ時,Eλ≥Eμ,②右連續性，當λn>λ，λn→λ時，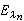
強收斂於Eλ,③規範性，當λ→-∞時，Eλ強收斂於0；當λ→+∞時,Eλ強收斂於I。稱滿足①～③的Eλ為相應於E 的譜系。反之，任何滿足①～③的函式Eλ必是惟一地相應於某個譜測度 E的譜系。對於有譜系的譜積分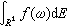
又常寫作
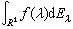或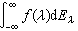
。 譜分解定理 設h是復希爾伯特空間,N是h上正常運算元。則必存在定義在複平面
C(視為R2)所有波萊爾集上譜測度E，使得
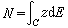。如果σ(N)是N 的譜集,則E的支集就是σ(N)，即
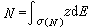。 正常運算元的譜分解定理實際上是 n維複線性空間上正常矩陣對角化理論在無限維復希爾伯特空間上的推廣。它刻畫了正常運算元的結構，許多正常運算元的重要性質可由它導出，例如①
λ∈σ(N)的充要條件是對任何λ的鄰域O，E(O)≠0；②λ是N 的特徵值的充要條件是單點集{λ}的譜測度E({λ})≠0;③λ是N的正則點的充要條件是存在λ的鄰域①，使得E(O)=0；當λ0是N的正則點時，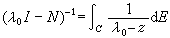
；④h上有界線性運算元 A和N可交換的充要條件是對任何M∈B，AE(M)=E(M)A等。 對於特殊的正常運算元，例如對酉運算元U，必存在【0，2π］上譜系
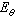（即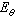是定義在［0，2π］上單調增加右連續，並且E0＝0，E2π＝I 的投影運算元值函式），使得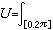
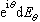；而對自共軛運算元A,必存在定義在R1上譜系Eλ,使得
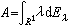。 運算元演算 對希爾伯特空間h上正常運算元N，有譜測度空間(σ(N),B,E)，這時對σ(N)上定義的復值有界波萊爾可測函式ƒ,定義
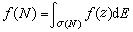,那么映射ƒ
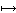ƒ(N)有如下性質： ① 埃爾米特性
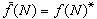，這裡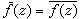
； ② 線性
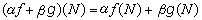； ③ 可乘性 (ƒg)(N)=ƒ(N)g(N)；
④
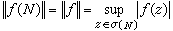。 此外,有譜映射定理：對希爾伯特空間h中的正常運算元N,若ƒ為σ(N)上的連續函式,那么有σ(ƒ(N))=ƒ(σ(N))。
廣義特徵分解 若希爾伯特空間h上自共軛運算元A滿足σp(A)=σ(A)（即A
的譜都是特徵值）。那么必有特徵展開式
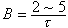，式中{ev}是h的完備就範正交系,並且ev是相應於特徵值λv的特徵向量。特徵展開式（離散和的形式）比譜分解式（連續和的形式）更為簡便。在吸收了廣義函式論方法的基礎上，引出了一般自共軛運算元的廣義特徵分解的概念。 設l2(Rn)是 n維歐幾里得空間Rn上關於勒貝格測度平方可積函式全體所成的希爾伯特空間。A是 L2(Rn)上的自共軛運算元，定義域D(A)包含基本函式空間K(見廣義函式)，而且是K到K中的連續線性運算元。又設當φ∈D(A)時,必有
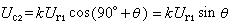,而且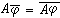
。A在K的共軛空間K┡上的共軛運算元A┡定義為：(A┡ψ,φ)=(ψ,Aφ)。如果對實數λ,有F∈K┡,F≠0，使A┡F=λF，就稱λ是A的廣義特徵值,F是相應的廣義特徵向量。當F∈D(A)時,廣義特徵值和廣義特徵向量就是通常的特徵值和特徵向量。 如果存在A的特徵值系{
λv}和相應的就範正交特徵向量系{ƒv}以及存在實直線上波萊爾集系{Bn}, Bn中每點λ為A的廣義特徵值，相應的廣義特徵向量為ƒλ,使得對任何φ，ψ∈K，(ƒλ, φ)是 Bn上波萊爾可測函式，且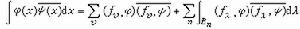
。那么就稱
組成了A的完備就範正交廣義特徵向量系。這時有如下的廣義特徵展開：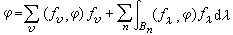 
,
。
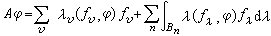λ)|λ∈(-∞,∞)}卻構成了A的完備就範正交廣義特徵向量系。對一般的希爾伯特空間中自共軛運算元,也有類似的廣義特徵分解。 簡言之，所謂廣義特徵展開，實質上就是原來在希爾伯特空間上不是特徵值的那些譜點，在適當擴大了的空間（相當於廣義函式空間）上變成了特徵值，並找到相應的（廣義）特徵向量和展開式。
巴拿赫空間上有界線性運算元的譜分解 對巴拿赫空間上線性運算元,一般說來,還沒有類似於正常運算元的譜分解定理這樣深刻的結果。作為希爾伯特空間上投影運算元的推廣,在巴拿赫空間有平行投影的概念。設X是巴拿赫空間,M和N是X的兩個閉子空間,如果任何x∈X可以唯一地表示為x=y+z,其中y∈M,z∈N,就稱X是M和N的直和，記為X=M+N。這時定義運算元E：Ex=y，稱運算元E是X到M上(平行於N)的平行投影，簡稱為X上投影運算元。E是X上投影運算元若且唯若E是X上有界的冪等運算元,即滿足E 2=E的有界線性運算元。
鄧福德－里斯分解定理 設T是巴拿赫空間X上的有界線性運算元，若σ是σ(T)的子集，且σ和σ┡=σ(T)\σ都是閉集,那么有X的直和分解X=M+N，使M,N都是T的不變子空間,而且σ(T｜M)=σ，σ(T｜N)=σ┡。這時存在一個包含 σ在其內部而σ┡在其外部的簡單的可求長的若爾當曲線C,
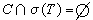,使X到M上平行於N的投影E正好是
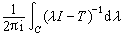。 解析函式演算 設T是巴拿赫空間X上有界線性運算元。ƒ是在 σ(T)的一個鄰域中解析的復值函式。取一個包含σ(T)於內部的簡單的可求長若爾當曲線C,C含於ƒ的解析區域中，定義
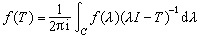。ƒ(T)是一個有界線性運算元,而且映射ƒ
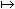ƒ(T)也有類似於正常運算元的運算元演算的性質②、③和對應的譜映射定理。 有關巴拿赫空間上全連續運算元譜理論和其他有關結果（見全連續運算元、譜運算元、線性運算元擾動理論）。
參考書目
N.Dunford and J.T.Schwartz,Linear Operators,Vol.1～2,Interscience, New York,1958，1963.
