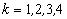抽象空間微分方程
正文
巴拿赫空間中的微分方程。是常微分方程理論在無限維空間中的發展,研究可數無窮個常微分方程、泛函微分方程需要巴拿赫空間或希爾伯特空間的理論。它也是用常微分方程的思想和方法,研究偏微分方程的重要工具。設Χ是巴拿赫空間,D是Χ中的開集,J是實軸上的開區間,函式ƒ∶J×D→Χ是連續的。微分方程
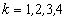 (1)
(1)
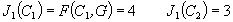 就稱 x=φ(t)是微分方程(1)的解。
就稱 x=φ(t)是微分方程(1)的解。 解的存在性 當ƒ關於 x滿足李普希茨條件(見常微分方程初值問題)時,利用逐次逼近法可以證明:對於給定的初值(t0,x0)∈J×D,微分方程(1)滿足初值條件
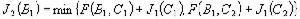 (2)
(2)
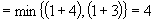 的數列全體所成的空間,它的元素x的範數(見巴拿赫空間)為‖x‖=sup│xk│。 在空間с0中考察含無窮個方程的常微分方程組
的數列全體所成的空間,它的元素x的範數(見巴拿赫空間)為‖x‖=sup│xk│。 在空間с0中考察含無窮個方程的常微分方程組 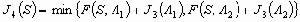 (3)
(3)
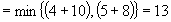 (4)
(4)
 )→【0,+
)→【0,+ )連續,而常微分方程
)連續,而常微分方程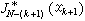 的以(t0,0)為初值的惟一解是ρ 呏0;那么微分方程(1)以(t0,x0)∈J×D為初值的解是存在的。它的證明需要利用紹德爾不動點定理(見不動點理論)。
的以(t0,0)為初值的惟一解是ρ 呏0;那么微分方程(1)以(t0,x0)∈J×D為初值的解是存在的。它的證明需要利用紹德爾不動點定理(見不動點理論)。 許多有關常微分方程組的定理,諸如初值問題解的惟一性定理等,都可移到巴拿赫空間中的微分方程(1)。
線性方程 當ƒ(t,x)呏A(t)x+b(t)時,方程(1)成為線性方程
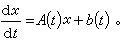 (5)
(5)
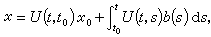
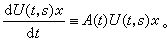 稱 U(t,s)是相應於(5)的發展運算元。特別,當A(t)呏A是Χ上的線性有界運算元時,
稱 U(t,s)是相應於(5)的發展運算元。特別,當A(t)呏A是Χ上的線性有界運算元時,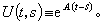 克列因還討論了A(·)具有周期ω的情形,推廣了周期係數線性常微分方程組的理論。對於非線性微分方程
克列因還討論了A(·)具有周期ω的情形,推廣了周期係數線性常微分方程組的理論。對於非線性微分方程 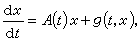 (6)
(6)
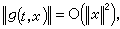 J=【0,+
J=【0,+ ),人們還討論了零解的穩定性,推廣了A.M.李亞普諾夫關於穩定性的有關結果(見常微分方程運動穩定性理論)。
),人們還討論了零解的穩定性,推廣了A.M.李亞普諾夫關於穩定性的有關結果(見常微分方程運動穩定性理論)。 但是,對於偏微分方程,例如熱傳導方程
 (7)
(7)
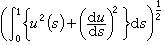 時所構成的希爾伯特空間,又記x(t)=u(t,·),b(t)=b(t,·),而當u(s)二階導數平方可積時,
時所構成的希爾伯特空間,又記x(t)=u(t,·),b(t)=b(t,·),而當u(s)二階導數平方可積時,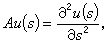 那么(7)可以化為Χ =H姲上的線性方程
那么(7)可以化為Χ =H姲上的線性方程 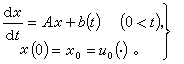 (8)
(8)
設線性運算元A的定義域D(A)是Χ中的稠密集,A還是閉運算元,如果當λ>β時A的預解運算元(λI-A)-1(見線性運算元)是Χ上的有界線性運算元,並且成立不等式
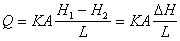
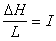 (9)
(9)
加藤敏夫、田辺広城以及∏.E.索伯列夫斯基等還討論了A(t)是Χ上的無界線性運算元時的微分方程(5),給出了發展運算元U(t,s)存在以及常數變易公式成立的條件。
為適應非線性拋物型偏微分方程理論、分布參數系統、控制理論等的需要,人們又進一步討論了半線性發展方程
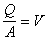 (10)
(10)
在抽象空間微分方程研究中,除解的存在性、惟一性、解對初值的連續性、常數變易公式外,還有人研究周期解的存在性、惟一性,解的穩定性,分歧現象,等等問題,並且研究解的全局結構、高階微分方程等。
關於解的概念,除前述的以強導數為依據的解的概念外,還有以弱導數為基礎的弱解的概念等。