隱函式
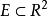隱函式存在定理
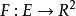隱函式存在定理設 ，函式 ，對於方程
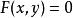隱函式存在定理（1）
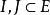隱函式存在定理
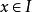隱函式存在定理
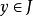隱函式存在定理
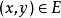隱函式存在定理
隱函式存在定理
隱函式存在定理如果存在集合 ，對任何 ，有唯一確定的 ，使得 ，且滿足方程（1），則稱方程（1）確定了一個定義在 上，值域含於 的隱函式。若把它記為
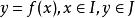隱函式存在定理則成立恆等式
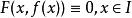隱函式存在定理
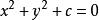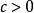隱函式存在定理
隱函式存在定理
隱函式存在定理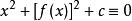
隱函式存在定理
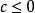隱函式存在定理隱函式必須在指出它的方程以及x,y的取值範圍後才有意義。當然，在不產生誤解的情況下，其取值範圍也可不必一一指明，此外，還需指出：並不是任一方程都能確定出隱函式，如方程： ，當 時，就不能確定任何函式 ，使得： ；而只有當 時，才能確定隱函式。
隱函式定理
存在唯一性定理
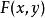隱函式存在定理若函式 滿足下列條件：
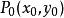隱函式存在定理
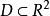隱函式存在定理(i) F 在以 為內點的某一區域 上連續
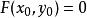隱函式存在定理(ii) （通常稱為初始條件）
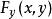隱函式存在定理(iii) F在D記憶體在連續的偏導數
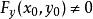隱函式存在定理(iv)
則
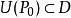隱函式存在定理
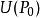隱函式存在定理
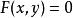隱函式存在定理 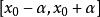隱函式存在定理
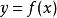隱函式存在定理
隱函式存在定理
隱函式存在定理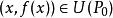
隱函式存在定理
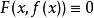隱函式存在定理
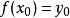隱函式存在定理1° 存在點 的某領域 ，在 上方程 唯一地決定了一個定義在某區間 上的隱函式 ，使得當 時， ，且 ， ；
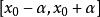隱函式存在定理 隱函式存在定理2° 在 上連續。
注意之處：
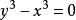隱函式存在定理
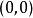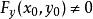隱函式存在定理 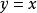隱函式存在定理
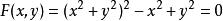隱函式存在定理
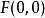隱函式存在定理
隱函式存在定理
隱函式存在定理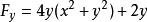
隱函式存在定理
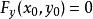隱函式存在定理（1）該定理的條件僅僅是充分的，例如方程 ，在點 不滿足條件(iv)（ ），但它仍能確定惟一的函式 。當然，由於條件(iv)不滿足，往往導致定理結論的失效，例如雙紐線，其方程為： 。由於 ， 與 均連續，故滿足定理(i)(ii)(iii)，但因 ，致使在原點的無論怎樣小的鄰域內都不可能存在唯一的隱函式。
隱函式存在定理（2）在定理的證明過程中，條件(iii)和(iv)只是用來保證存在 的某一鄰域，在此鄰域內F關於變數y是嚴格單調的。
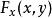隱函式存在定理
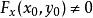隱函式存在定理
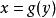隱函式存在定理（3）如果把定理的條件(iii)、(iv)改為 連續，且 ，這時，結論是存在惟一的連續函式
可微性定理
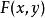隱函式存在定理 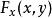隱函式存在定理 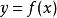隱函式存在定理 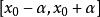隱函式存在定理
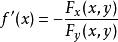隱函式存在定理設 滿足隱函式存在惟一性定理中的條件(i)-(iv)，又設在D上還存在連續的偏導數 ，則由方程(1)所確定的隱函式 在其定義域 上有連續導函式，且
n元隱函式
n元隱函式的惟一存在與連續可微性定理：
若
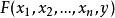隱函式存在定理
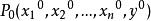隱函式存在定理
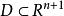隱函式存在定理(i)函式在以點為內點的區域 上連續，
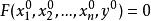隱函式存在定理(ii)
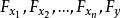隱函式存在定理(iii)偏導數在D上存在且連續
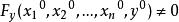隱函式存在定理(iv)
則
隱函式存在定理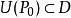 隱函式存在定理 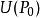隱函式存在定理
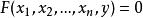隱函式存在定理
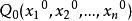隱函式存在定理
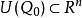隱函式存在定理
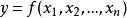隱函式存在定理1° 存在點 的某鄰域，在上方程惟一地確定了一個定義在的某鄰域 上的n元連續函式（隱函式），使得：
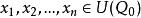隱函式存在定理當 時
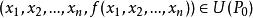隱函式存在定理且
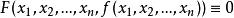隱函式存在定理
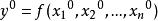隱函式存在定理 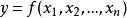隱函式存在定理
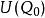隱函式存在定理
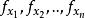隱函式存在定理2°在上有連續偏導數，而且
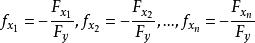隱函式存在定理隱函式組
若
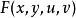隱函式存在定理
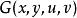隱函式存在定理
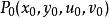隱函式存在定理
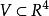隱函式存在定理(i)與在以點 為內點的區域 上連續
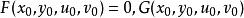隱函式存在定理(ii)（初始條件）
隱函式存在定理
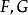隱函式存在定理(iii)在 上 具有一階連續偏導數
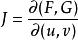隱函式存在定理 隱函式存在定理(iv) 在點 不等於零
則
隱函式存在定理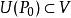
隱函式存在定理 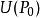隱函式存在定理
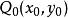隱函式存在定理 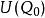隱函式存在定理1° 存在點的某一（四維空間）鄰域，在上，方程組（1）惟一地確定了定義在點的某一（二維空間）鄰域上的兩個二元隱函式
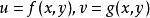隱函式存在定理使得：
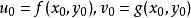隱函式存在定理
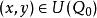隱函式存在定理，且當 時
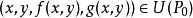隱函式存在定理
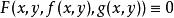隱函式存在定理
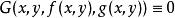隱函式存在定理
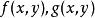隱函式存在定理 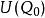隱函式存在定理2°在上連續
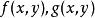隱函式存在定理 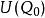隱函式存在定理3°在上有一階偏導數，且
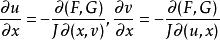隱函式存在定理
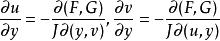隱函式存在定理