例子
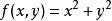 隱函式定理
隱函式定理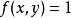 隱函式定理
隱函式定理定義函式 ,那么方程 的所有解的集合構成單位圓。
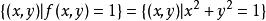 隱函式定理
隱函式定理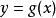 隱函式定理
隱函式定理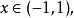 隱函式定理
隱函式定理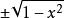 隱函式定理
隱函式定理( )。圓上的點是無法用統一的方法表示成 的形式的,因為每個 都有兩個 y的值與之對應,即 。
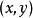 隱函式定理
隱函式定理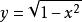 隱函式定理
隱函式定理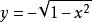 隱函式定理
隱函式定理然而,局部地用 x來表示y是可以的。給定圓上一點 ,如果y>0,也就是說這點在圓的上半部分的話,在這一點附近y可以寫成關於x的函式: 。如果y<0,附近的y也可以寫成關於x的函式: 。
但是,在點(1,0)的附近,y無法寫成關於x的函式,因為(1,0)的每一個鄰域中都包含了上半圓和下半圓的點,於是對於附近的每一個x,都有兩個 y的值與之對應。
定理的敘述
設 f: R→ R為一個連續可微函式。這裡 R被看作是兩個空間的直積: R× R,於是 R中的一個元素寫成 ( x, y)=( x,..., x, y,..., y)的形式。
對於任意一點( a, b)=( a,..., a, b,..., b)使得 f( a, b)=0,隱函式定理給出了能否在( a, b)附近定義一個 y關於 x的函式 g,使得只要: f( x, y)=0,就有 y= g( x)的充分條件。這樣的函式 g存在的話,嚴格來說,就是說存在 a和 b的鄰域 U和 V,使得 g的定義域是: g: U→ V,並且 g的函式圖像滿足:
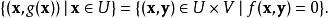 隱函式定理
隱函式定理隱函式定理說明,要使的這樣的函式 g存在,函式f的雅可比矩陣一定要滿足一定的性質。對於給定的一點 ( a, b), f的雅可比矩陣寫作:
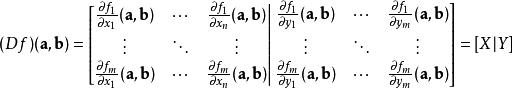 隱函式定理
隱函式定理其中的矩陣X是 f關於 x的偏微分,而Y是f關於y的偏微分。隱函式定理說明了:如果Y是一個可逆的矩陣的話,那么滿足前面性質的U、 V和函式 g就會存在。概括地寫出來,就是:
設 f: R→ R為連續可微函式,並令 R中的坐標記為 ( x, y)。給定一點 ( a,..., a, b,..., b)=( a,b)使得 f( a, b)= c,其中 c∈ R。如果矩陣[(∂ f/∂ y)(a,b)]是可逆矩陣的話,那么存在 a的鄰域 U、 b的鄰域 V以及同樣是連續可微的函式 g: U→ V,滿足
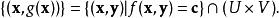 隱函式定理
隱函式定理一般情形
設 E、E和F是三個巴拿赫空間,而U、V分別是E、E上的兩個開集。設函式:
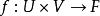 隱函式定理
隱函式定理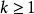 隱函式定理
隱函式定理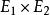 隱函式定理
隱函式定理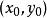 隱函式定理
隱函式定理是一個C 的函式(見光滑函式),其中 ,並且對於 中的一點 ,滿足:
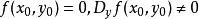 隱函式定理
隱函式定理那么有如下結論:
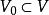 隱函式定理
隱函式定理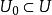 隱函式定理
隱函式定理 隱函式定理
隱函式定理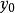 隱函式定理
隱函式定理存在 的鄰域以及 的鄰域;
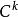 隱函式定理
隱函式定理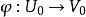 隱函式定理
隱函式定理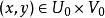 隱函式定理
隱函式定理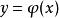 隱函式定理
隱函式定理存在一個 的函式: ,使得對任意 ,只要 f(x,y)=0,就有 。

