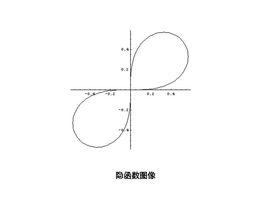
定義
隱函式是由隱式方程所隱含定義的函式。設F(x,y)是某個定義域上的函式。如果存在定義域上的子集D,使得對每個x屬於D,存在相應的y滿足F(x,y)=0,則稱方程確定了一個隱函式。記為y=y(x)。 顯函式是用y=f(x)來表示的函式,顯函式是相對於隱函式來說的。
求導法則
對於一個已經確定存在且可導的情況下,我們可以用複合函式求導的鏈式法則來進行求導。在方程左右兩邊都對x進行求導,由於y其實是x的一個函式,所以可以直接得到帶有 y' 的一個方程,然後化簡得到 y' 的表達式。
隱函式導數的求解一般可以採用以下方法:
方法①:先把隱函式轉化成顯函式,再利用顯函式求導的方法求導;
方法②:隱函式左右兩邊對x求導(但要注意把y看作x的函式);
方法③:利用一階微分形式不變的性質分別對x和y求導,再通過移項求得的值;
方法④:把n元隱函式看作(n+1)元函式,通過多元函式的偏導數的商求得n元隱函式的導數。
舉個例子,若欲求z = f(x,y)的導數,那么可以將原隱函式通過移項化為f(x,y,z) = 0的形式,然後通過(式中F'y,F'x分別表示y和x對z的偏導數)來求解。
推理過程
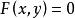 隱函式
隱函式一個函式 y= ƒ( x),隱含在給定的方程 中,作為這方程的一個解(函式)。例如
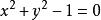 隱函式
隱函式(1)
如果不限定函式連續,則式中正負號可以隨 x而變,因而有無窮個解;如果限定連續,則只有兩個解(一個恆取正號,一個恆取負號);如果限定可微,則要排除 x=±1,因而函式的定義域應是開區間(-1< x<1),但仍然有兩個解;如果還限定在適合原方程的一個點( x, y)=( x, y)的鄰近範圍內,則只有一個惟一的解(當起點( x, y)在上半平面時取正號,在下半平面時取負號)。
微分學中主要考慮函式 z= F( x, y)與 y= ƒ( x)都連續可微的情形。
這時可以利用複合函式的微分法對方程(1)直接進行微分:
 隱函式
隱函式(2)
可見,即使在隱函式 y= ƒ( x)難於解出的情形,也能夠直接算出它的導數,唯一的條件是
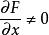 隱函式
隱函式(3)
隱函式理論的基本問題就是:在適合原方程(1)的一個點的鄰近範圍內,在函式 F( x, y)連續可微的前提下,什麼樣的附加條件能使得原方程(1)確定一個惟一的函式 y= ƒ( x),不僅單值連續,而且連續可微,其導數由(2)完全確定。隱函式存在定理就用於斷定(3)就是這樣的一個條件,不僅必要,而且充分。
示例
設方程P(x, y)=0確定y是x的函式,並且可導。如今可以利用複合函式求導公式求出隱函式y對x的導數。
例1 方程 x +y -r =0確定了一個以x為自變數,以y為因變數的數,為了求y對x的導數,將上式兩邊逐項對x求導,並將y 看作x的複合函式,則有:
(x )+ (y )-(r )=0
即 2x+2yy'=0
於是得y'=-x/y 。
從上例可以看到,在等式兩邊逐項對自變數求導數,即可得到一個包含y'的一次方程, 解出y'即為隱函式的導數。
例2 求由方程y =2px所確定的隱函式y=f(x)的導數。
解: 將方程兩邊同時對x求導,得:
2yy'=2p
解出y'即得
y'=p/y
例 3 求由方程y=x ln y所確定的隱函式y=f(x)的導數。
解:將方程兩邊同時對x求導,得
y’=ln y+xy' /y
解出y'即得 。