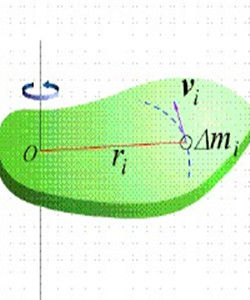
基本簡介
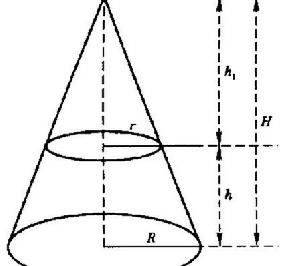轉動慣量電磁系儀表的指示系統，因線圈的轉動慣量不同，可分別用於測量微小電流（檢流計）或電量（衝擊電流計）。在發動機葉片、飛輪、陀螺以及人造衛星的外形設計上，精確地測定轉動慣量，都是十分必要的。
對於質量分布均勻，外形不複雜的物體可以從它的外形尺寸的質量分布用公式計算出相對於某一確定轉軸的轉動慣量。對於幾何形狀簡單、質量分布均勻的剛體可以直接用公式計算出它相對於某一確定轉軸的轉動慣量。而對於外形複雜和質量分布不均勻的物體只能通過實驗的方法來精確地測定物體的轉動慣量，因而實驗方法就顯得更為重要。
測定方法
測定剛體轉動慣量的方法很多，常用的有三線擺、扭擺、復擺等。本實驗採用的是三線擺，是通過扭轉運動測定物體的轉動慣量，其特點是無力圖像清楚、操作簡便易行、適合各種形狀的物體，如機械零件、電機轉子、槍炮彈丸、電風扇的風葉等的轉動慣量都可用三線擺測定。這種實驗方法在理論和技術上有一定的實際意義本實驗的目的就是要求學生掌握用三線擺測定物體轉動慣量的方法，並驗證轉動慣量的平行軸定理。動力學公式
上面給出的是轉動慣量的定義和計算公式。下面給出一些（定軸轉動的）剛體動力學公式。角加速度與合外力矩的關係：
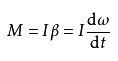
角動量：
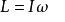
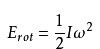
張量定義
剛體繞某一點轉動的慣性可由更普遍的慣性張量描述。慣性張量是二階對稱張量，它完整地刻畫出剛體繞通過該點任一軸的轉動慣量的大小。出於簡單的角度考慮，這裡僅給出繞質心的轉動慣量張量的定義及其在力矩方程中的表達式。設有一個剛體A,其質心為C,剛體A繞其質心C的轉動慣量張量定義為：
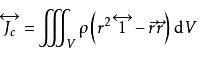
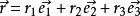，是剛體質心C到剛體上任一點B的矢徑；表達式：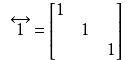
轉動慣量張量的力矩方程
設剛體A所受到的繞其質心C的合力矩矢量為：
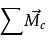，剛體A在慣性系下的角速度矢量為，角加速度矢量為
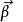，A繞其質心的轉動慣量張量為
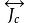，則有如下的力矩方程：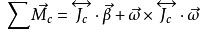
轉動慣量張量
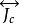是一個二階張量，雖然在標架
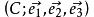下它有九個分量，但是因為它是一個對稱張量，故其實際獨立的分量只有六個。實驗測定
三線擺實驗原理
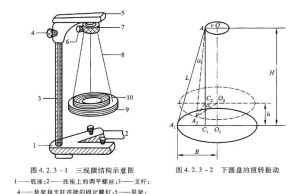實驗原理圖當上、下圓盤水平三線等長時，將上圓盤繞豎直的中心軸線O1O轉動一個小角度，藉助懸線的張力使懸掛的大圓盤繞中心軸O1O作扭轉擺動。同時，下圓盤的質心O將沿著轉動軸升降，=H是上、下圓盤中心的垂直距離；=h是下圓盤在振動時上升的高度；是上圓盤的半徑；是下圓盤的半徑；α是扭轉角。
由於三懸線能力相等，下圓盤運動對於中心軸線是對稱的，僅分析一邊懸線的運動。用L表示懸線的長度，當下圓盤扭轉一個角度α時，下圓盤的懸線點移動到，下圓盤上升的高度為，與其他幾何參量的關係可作如下考慮。
實驗內容
1、測定儀器常數。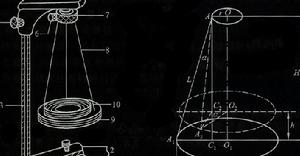
轉動慣量2、測量下圓盤的轉動慣量，並計算其不確定度
轉動三線擺上方的小圓盤，使其繞自身軸轉一角度α，藉助線的張力使下圓盤作扭擺運動，而避免產生左右晃動。自己擬定測的方法，使周期的測量不確定度小於其它測量量的不確定度。利用式，求出，並推導出不確定度傳遞公式，計算的不確定度。
3、測量圓環的轉動慣量
在下圓盤上放上待測圓環，注意使圓環的質心恰好在轉動軸上，測量系統的轉動慣量。測量圓環的質量和內、外直徑。利用式求出圓環的轉動慣量。並與理論值進行比較，求出相對誤差。
4、驗證平行軸定理
將質量和形狀尺寸相同的兩金屬圓柱重疊起來放在下圓盤上，注意使質心與下圓盤的質心重合。測量轉動軸通過圓柱質心時，系統的轉動慣量。然後將兩圓柱對稱地置於下圓盤中心的兩側。測量此時系統的轉動慣量。測量圓柱質心到中心轉軸的距離計算，並與測量值比較。
相關定理
平行軸定理
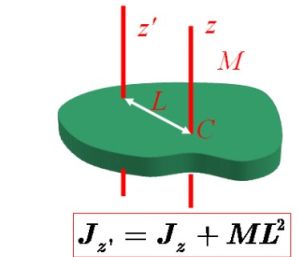平行軸定理利用平行軸定理可知，在一組平行的轉軸對應的轉動慣量中，過質心的軸對應的轉動慣量最小。垂直軸定理
一個平面剛體薄板對於垂直它的平面軸的轉動慣量，等於繞平面內與垂直軸相交的任意兩正交軸的轉動慣量之和。
表達式:Iz=Ix+Iy
剛體對一軸的轉動慣量，可折算成質量等於剛體質量的單個質點對該軸所形成的轉動慣量。由此折算所得的質點到轉軸的距離 ，稱為剛體繞該軸的迴轉半徑κ，其公式為_____，式中M為剛體質量；I為轉動慣量。
轉動慣量的量綱為L2M，在SI單位制中，它的單位是kg·m2。 剛體繞某一點轉動的慣性由更普遍的慣量張量描述。慣量張量是二階對稱張量，它完整地刻畫出剛體繞通過該點任一軸的轉動慣量的大小。 補充對轉動慣量的詳細解釋及其物理意義：先說轉動慣量的由來，先從動能說起大家都知道動能E=(1/2)mv^2，而且動能的實際物理意義是：物體相對某個系統運動的實際能量，（P勢能實際意義則是物體相對某個系統運動的可能轉化為運動的實際能量的大小）。
E=(1/2)mv^2 （v^2為v的2次方） 把v=wr代入上式 (w是角速度,r是半徑，在這裡對任何物體來說是把物體微分化分為無數個質點，質點與運動整體的重心的距離為r,而再把不同質點積分化得到實際等效的r) 得到E=(1/2)m(wr)^2 由於某一個對象物體在運動當中的本身屬性m和r都是不變的，所以把關於m、r的變數用一個變數K代替,
K=mr^2 ，得到E=(1/2)Kw^2 ，K就是轉動慣量，分析實際情況中的作用相當於牛頓運動平動分析中的質量的作用，都是一般不輕易變的量。
垂直軸定理
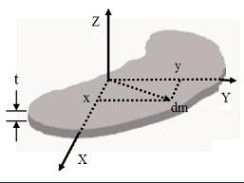薄板的垂直軸定理表達式:
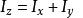
對於非平面薄板狀的剛體,亦有如下垂直軸定理成立:
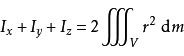
剛體對一軸的轉動慣量，可折算成質量等於剛體質量的單個質點對該軸所形成的轉動慣量。由此折算所得的質點到轉軸的距離，稱為剛體繞該軸的迴轉半徑κ，其公式為
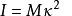，式中M為剛體質量；I為轉動慣量。除以上兩定理外，常用的還有伸展定則。伸展定則闡明，如果將一個物體的任何一點，平行地沿著一支直軸作任意大小的位移，則此物體對此軸的轉動慣量不變。我們可以想像，將一個物體，平行於直軸地，往兩端拉開。在物體伸展的同時，保持物體任何一點離直軸的垂直距離不變，則伸展定則闡明此物體對此軸的轉動慣量不變。伸展定則通過轉動慣量的定義式就可以簡單得到。計算公式
轉動慣量和質量一樣，是迴轉物體保持其勻速圓周運動或靜止的特性，用字母J表示。
對於細桿
當迴轉軸過桿的中點並垂直於桿時；其中m是桿的質量，L是桿的長度。
當迴轉軸過桿的端點並垂直於桿時；
其中m是桿的質量，L是桿的長度。
對於圓柱體
部分勻質幾何體的轉動慣量當迴轉軸是圓柱體軸線時；
其中m是圓柱體的質量，r是圓柱體的半徑。
對於細圓環
對於細圓環當迴轉軸通過環邊緣且與環面垂直時；
沿環的某一直徑；
R為其半徑。
對於薄圓盤
當迴轉軸通過中心與盤面垂直時；當迴轉軸通過邊緣與盤面垂直時；
R為其半徑。
對於空心圓柱
當迴轉軸為對稱軸時。（注意這裡是加號不是減號，容易記錯。可以代入的極端情況進行驗證，此時圓柱退化為柱面。）
R1和R2分別為其內外半徑。
對於球殼
當迴轉軸為中心軸時，當迴轉軸為球殼的切線時，
R為球殼半徑。
對於實心球體
當迴轉軸為球體的中心軸時，當迴轉軸為球體的切線時，
R為球體半徑。
對於立方體
當迴轉軸為其中心軸時，當迴轉軸為其棱邊時，
當迴轉軸為其體對角線時，
L為立方體邊長。
對於長方體
當迴轉軸為其中心軸時，式中l1和l2是與轉軸垂直的長方形的兩條邊長。例題
已知：一個直徑是80的軸，長度為500，材料是鋼材。計算一下，當在0.1秒內使它達到500轉/分的速度時所需要的力矩？
分析：知道軸的直徑和長度，以及材料，我們可以查到鋼材的密度，進而計算出這個軸的質量m，由公式ρ=m/v可以推出m=ρv=ρπr²L.
根據在0.1秒達到500轉/分的角速度，我們可以算出軸的角加速度β=△ω/△t=（500rad/min）/0.1s
電機軸我們可以認為是圓柱體過軸線，所以J=mr²/2。
所以M=Jβ
=（mr²/2）（△ω/△t）
=ρπr^2hr²/2△ω/△t
=7.8×10³×3.14×0.04²×0.5×0.04²/2×500×2π/60/0.1
=8.203145
單位kg·m²/s²=N·m
