復擺

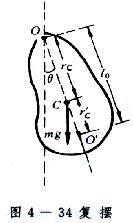
在重力作用下，能繞通過自身某固定水平軸擺動的剛體。即復擺是一剛體繞固定的水平軸在重力的作用下作微小擺動的動力運動體系。又稱物理擺。

復擺

復擺

compound pendulum

又稱物理擺。

復擺的轉軸與過剛體質心C並垂直於轉軸的平面的交點O稱為支點或懸掛點。擺動過程中，復擺只受重力和轉軸的反作用力，而重力矩起著回復力矩的作用。設質量為m的剛體繞轉軸的轉動慣量為I，支點至質心的距離為s，則復擺微幅振動的周期如圖，式中g為重力加速度。它相當於擺長l=I/ms的單擺作微幅振動的周期。在OC的延長線上取O′點使OO′=l（l稱等價擺長）則此點稱為復擺的擺動中心。支點和擺動中心可互換位置而不改變復擺的周期。知道T和l，就可由周期公式求出重力加速度g。當復擺受到一個衝量作用時，會在支點上引起碰撞反力。若轉軸是剛體對支點的慣量主軸，外衝量垂直於支點和質心的連線OC且作用於擺動中心 O′上，則支點上的碰撞反力為零。因此，復擺的擺動中心又稱撞擊中心。機器中有些必須經受碰撞的轉動件，如離合器、衝擊擺錘等，為防止巨大瞬時力對軸承的危害，應使碰撞衝擊力通過撞擊中心。