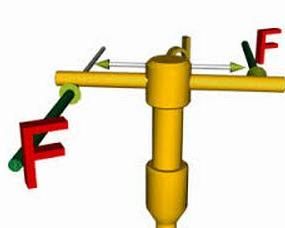
定義
大小相等、方向相反,但作用線不在同一直線上的一對力(如圖上的F和F′)。力偶能使物體產生純轉動效應。例如,用雙手使用絲錐,施加的力偶對絲錐不會產生橫向側壓力,這樣鑽得的孔才能與表面垂直。力偶的二力對空間任一點之矩的和是一常量,稱為力偶矩。用靜力學公理和幾何學可證明:一力偶可用與其作用面相平行和力偶矩相等的另一力偶代替,而不改變其對剛體的轉動作用。由於力偶的作用平面具有方向性,須引入一空間力偶矩矢T,其方向線與力偶作用平面垂直,並按右手螺鏇定則確定其指向(見圖)。T的大小等於力和力偶臂(力偶的二力線間的垂直距離)的乘積。由於力偶的作用面可在剛體上自由平移,所以剛體上的力偶矩矢是自由矢,即它的作用點可以是剛體上的任一點。如力偶作用在變形體上,力偶矩矢就不可自由平移,因為這樣會產生不同的扭轉效應。受力偶作用的物體,會產生角加速度,不能用一個力來平衡,因為一個力具有主矢,但由一個力偶所組成的力系,其主矩不為零,而主矢為零。力偶矩的量綱和單位與力矩的相同。作用在剛體上的兩個或兩個以上的力偶組成力偶系。若力偶系中各力偶都位於同一平面內,則為平面力偶系,否則為空間力偶系。力偶既然不能與一個力等效,力偶系簡化的結果顯然也不能是一個力,而仍為一力偶,此力偶稱為力偶系的合力偶。
三大要素
力偶在平面內的轉向不同,其作用效應也不相同。因此,平面力偶對物體的作用效應,由以下兩個因素決定:
1.力偶矩的大小。2.力偶的轉向。
平面力偶可以視為代數量,以M或M(F,F')表示,即
M=±Fd (2-11)
於是可得結論:力偶矩是一個代數量,其絕對值等於力的大小與力偶臂的乘積,正負號表示力偶的轉向:一般以逆時針為正,反之為負。力偶矩的單位為與力矩相同,也是N·m。
注釋
基本注釋
一般,將作用於同一剛體上的大小相等,方向相反但不共線的兩個平行力組成的力系,稱為力偶,力偶為矢量,力偶是一種只有合轉矩(所有轉矩的總合),沒有合力的力系統。因此,它又稱為純轉矩。作用於物體,力偶能夠使物體完全不呈現任何平移運動,只呈現純鏇轉運動。最簡單的力偶是由兩隻大小相等,方向相反的力構成的,力偶的國際單位制是牛頓*米。力偶是指兩個大小相等方向相反的特殊力系。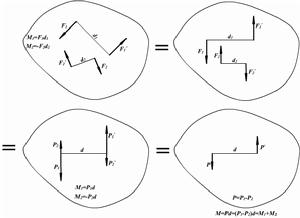
基本性質
性質1:力偶沒有合力,所以力偶不能用一個力來代替,也不能與一個力來平衡。解釋:從力偶的定義和力的合力投影定理可知,力偶中的二力在其作用面內的任意坐標軸上的投影的代數和恆為零,所以力偶沒有合力,力偶對物體只能有轉動效應,而一個力在一般情況下對物體有移動和轉動兩種效應。因此,力偶與力對物體的作用效應不同,所以其不能與一個力等效,也不能用一個力代替,也就是說力偶不能和一個力平衡,力偶只能和轉向相反的力偶平衡。
性質2:力偶對其作用面內任一點之矩恆等於力偶矩,且與矩心位置無關。
性質3:在同一平面內的兩個力偶,如果它們的力偶矩大小相等,轉向相同,則這兩個力偶等效。稱為力偶的等效條件。
等效理論
作用在同一剛體上的兩力偶,如果力偶矩矢相等,則兩力偶等效。