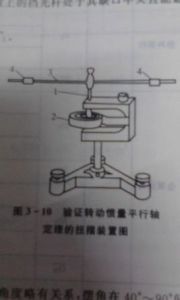
平行軸定理

平行軸定理（parallel axis theorem）能夠很簡易地，從剛體對於一支通過質心的直軸（質心軸）的轉動慣量，計算出剛體對平行於質心軸的另外一支直軸的轉動慣量。讓代表剛體對於質心軸的轉動慣量、 代表剛體的質量、 代表另外一支直軸 z'-軸與質心軸的垂直距離。平行軸定理、垂直軸定理、伸展定則，這些工具都可以用來求得許多不同形狀的物體的轉動慣量。因雅各·史丹納 (Jakob Steiner) 而命名，史丹納定理所指的幾個理論，其中一個理論就是平行軸定理。

基本信息

• 名稱：平行軸定理
• 外文名稱：parallel axis theorem
• 作者： 因雅各·史丹納

平行軸定理

設通過剛體質心的軸線為Z軸，剛體相對於這個軸線的轉動慣量為Jc。如果有另一條軸線Z‘與通過質心的軸線Z平行，那么，剛體對通過Z軸的轉動慣量為 J=Jc+md^2

式中m為剛體的質量，d為兩平行軸之間的距離。

上述關係叫做轉動慣量的平行軸定理。

驗證平行軸定理的方法

方法一

剛體對任意軸的轉動慣量，等於剛體對通過質心並與該軸平行的軸的轉動慣量，再加上剛體質量與兩軸之間距離平方的乘積，此為平行軸定理.關於此定理的驗證，採用三線擺和剛體轉動實驗儀來驗證。在這裡利用復擺驗證平行軸定理的方法。

一 實驗方法及公式推導

一個圍繞定軸擺動的剛體就是復擺，當擺動的振幅甚小時，其振動周期 T 為

式中J為復擺對以O 為軸轉動時的轉動慣量，m為復擺的質量，g為當地的重力加速度，h為擺的支點O到擺的質心G的距離。又設復擺對通過質心G平行O軸的軸轉動時的轉動慣量為JG，根據平行軸定理得:

而JG又可寫成 JG= m k 2,k 就是復擺的迴轉半徑，由此可將⑴式改成為

整理⑶式得：

當 h= h1 時，I1= JG + mh12，式中h1為支點O1到擺的質心G的距離，J1是以O1為軸時的轉動慣量。同理有：

⑷- ⑸得：

上式反映出轉軸位置對轉動的影響，也是對平行軸定理的檢驗。在⑹式中令 y= T2h- T12h1，x = h2-h12，則⑹式變為

從測量可得出n組（x,y)值，用最小二乘法求出擬合直線y= a+ bx及相關係數r，若r接近於1，說明x與y二者線性相關，平行軸定理得到驗證；或作T2h- T12h1對h2-h12圖線，若到檢驗為一直線，平行軸定理亦得

方法二

測量舉例

1） 測量步驟

a. 測定重心G的位置SG

將復擺水平放在支架的刀刃上，利用槓桿原理尋找G點的位置

b. 量出各支點對應的h值

c. 測出復擺繞各支點擺動的周期T擺角小於 （5°改變支點10次)

2） 數據記錄

各支點對應的 h 值及周期T見表1

3） 數據處理

取 h1= 6 cm,T1= 1.51 s，根據測量數據可得出10組（x,y）值，見表2

根據最小二乘法求出參數 a,b，得出

a= 21×10-2 cm ·s 2,Sa = 18×1010-2 cm s 2

b= 0. 0411s 2 ·cm-1,Sb = 0. 0005 s 2 ·cm-1

r= 0. 999375

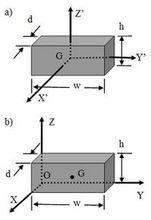平行軸定理

在此實驗中，誤差的主要來源是偶然誤差，所以只計算A類標準不確定度作為總的不確定度，略去B類不確定度。結果a,b 的不確定度為：

u(a) = 18×10-2 cm ·s 2

u (b) = 0. 0005 s 2 ·cm-1

最後結果為：

a= （21±18） ×10-2 cm ·s 2

b= 0. 0411±0. 0005 s 2 ·cm-1

r= 0. 999375

從最後結果可以看出，x 與 y 二者完全線性相關，平行軸定理得到驗證