貨幣乘數:所謂貨幣乘數也稱貨幣擴張係數或貨幣擴張乘數，是指在基礎貨幣（高 -百科知識中文網

簡介

貨幣乘數是指貨幣供給量對基礎貨幣的倍數關係，簡單地說，貨幣乘數是一單位準備金所產生的貨幣量。

完整的貨幣（政策）乘數的計算公式是：k=（Rc+1）/(Rd+Re+Rc)。其中Rd、Re、Rc分別代表法定準備金率、超額準備率和現金在存款中的比率。而貨幣（政策）乘數的基本計算公式是：貨幣供給/基礎貨幣。貨幣供給等於通貨（即流通中的現金）和活期存款的總和；而基礎貨幣等於通貨和準備金的總和。

效應

在貨幣供給過程中，中央銀行的初始貨幣提供量與社會貨幣最終形成量之間客觀存在著數倍擴張（或收縮）的效果或反應，這即所謂的乘數效應。貨幣乘數主要由通貨—存款比率和準備—存款比率決定。通貨—存款比率是流通中的現金與商業銀行活期存款的比率。
它的變化反向作用於貨幣供給量的變動，通貨—存款比率越高，貨幣乘數越小；通貨—存款比率越低，貨幣乘數越大。準備—存款比率是商業銀行持有的總準備金與存款之比，準備—存款比率也與貨幣乘數有反方向變動的關係。
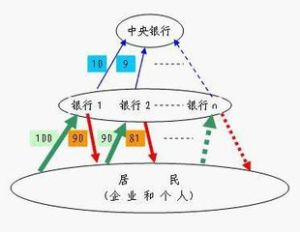
先假設最低準備金率是20%，也就是說當銀行得到100元的存款時它必須留存20元，只能貸出80元，其次假設銀行會放足80元。
現在有某君A往銀行里存了100元，銀行再將其中的80元放貸給B，如果B把貸來的80元又全部存入銀行，銀行再將其中的64元貸給了C，C又把64元存入銀行，銀行再向D貸出51.2元...依此類推，央行最先向市場投放了100元，市場上最後多的貨幣會是100+80+64+51.2+...
解這個數列的值是500，其實就是100*（1/0.2）=500。
也就是實際的貨幣投放量。這裡的1/0.2就是貨幣乘數也就是1除以法定準備金率。
中央銀行的初始貨幣提供量與社會貨幣最終形成量之間存在數倍擴張（或收縮）的效果或反應，即乘數效應。

決定因素

銀行提供的貨幣和貸款會通過數次存款、貸款等活動產生出數倍於它的存款，即通常所說的派生存款。貨幣乘數的大小決定了貨幣供給擴張能力的大小。而貨幣乘數的大小又由以下因素決定：

現金比率（k）
現金比率是指流通中的現金與商業銀行活期存款的比率。現金比率的高低與貨幣需求的大小正相關。因此，凡影響貨幣需求的因素，都可以影響現金比率。例如銀行存款利息率下降，導致生息資產收益減少，人們就會減少在銀行的存款而寧願多持有現金，這樣就加大了現金比率。現金比率與貨幣乘數負相關，現金比率越高，說明現金退出存款貨幣的擴張過程而流入日常流通的量越多，因而直接減少了銀行的可貸資金量，制約了存款派生能力，貨幣乘數就越小。

即流通中的現金占商業銀行活期存款的比率。k值大小，主要取決於社會公眾的資產偏好。一般來講，影響k值的因素有：

（1）公眾可支配的收入水平的高低。可支配收入越高，需要持有現金越多；反之，需持有現金越少。

（2）公眾對通貨膨脹的預期心理。預期通貨膨脹率高，k值就高；反之，k值則低。

（3）社會支付習慣、銀行業信用工具的發達程度、社會及政治的穩定性、利率水平等都影響到k值的變化。

在其他條件不變的情況下，k值越大，貨幣乘數越小；反之，貨幣乘數越大。

超額準備金率（e）
商業銀行保有的超過法定準備金的準備金與存款總額之比，稱為超額準備金率。顯而易見，超額準備金的存在相應減少了銀行創造派生存款的能力，因此，超額準備金率與貨幣乘數之間也呈反方向變動關係，超額準備金率越高，貨幣乘數越小；反之，貨幣乘數就越大。

e值的大小完全取決於商業銀行自身的經營決策。商業銀行願意持有多少超額準備金，主要取決於以下幾個因素：

（1）持有超額準備金的機會成本大小，即生息資本收益率的高低。

（2）借入準備金的成本大小，主要是中央銀行再貼現率的高低。如果再貼現率高，意味著借入準備金成本高，商業銀行就會保留較多超額準備金，以備不時之需；反之，就沒有必要保留較多的超額準備金。

（3）經營風險和資產的流動性。如果經營風險較大，而現有資產的流動性又較差，商業銀行就有必要保留一定的超額準備金，以備應付各種風險。

一般來說，e值越大，貨幣乘數越小；反之e值越小，貨幣乘數越大。活期存款法定準備金率（rd）和定期存款法定準備金率rt）rd和rt的大小是由中央銀行直接決定的。若rd、rt值大，貨幣乘數就小；反之，若rd、rt值小，貨幣乘數則大。

定期存款與活期存款間的比率
定期存款與活期存款的法定準備金率均由中央銀行直接決定。通常，法定準備金率越高，貨幣乘數越小；反之，貨幣乘數越大。
由於定期存款的派生能力低於活期存款，各國中央銀行都針對商業銀行存款的不同種類規定不同的法定準備金率，通常定期存款的法定準備金率要比活期存款的低。這樣即便在法定準備金率不變的情況下，定期存款與活期存款間的比率改變也會引起實際的平均法定存款準備金率改變，最終影響貨幣乘數的大小。一般來說，在其他因素不變的情況下，定期存款對活期存款比率上升，貨幣乘數就會變大；反之，貨幣乘數會變小。總之，貨幣乘數的大小主要由法定存款準備金率、超額準備金率、現金比率及定期存款與活期存款間的比率等因素決定。而影響我國貨幣乘數的因素除了上述四個因素之外，還有財政性存款、信貸計畫管理兩個特殊因素。
綜合上述分析說明，貨幣乘數的大小是由k、t、e、rd、rt等因素決定的。也就是說，貨幣乘數受到銀行、財政、企業、個人個人各自行為的影響。而貨幣供應量的另一個決定因素即基礎貨幣，是由中央銀行直接地控制和供應的。

確定方法

假定活期存款為D，流通中的現金為C，則一定時期內的貨幣供應量M1為：

M1=D+C（1）因為M1是流通中的貨幣量，是最重要的貨幣層次，我們在這裡考察M1的貨幣乘數決定問題。

假定商業銀行的存款準備金總額為A，它由法定準備金和超額準備金E兩部分組成。假定活期存款準備率為rd，定期存款準備率為rt，定期存款為T，則：

A=D.rd+T.rt+E（2）

假定流通中的現金C與活期存款、定期存款T與活期存款、超額準備金E與活期存款分別維持較穩定的比例關係，其係數分別用足k、t、e表示，則：

C=D.k（3）
T=D.t（4）
E=D.e（5）
基礎貨幣B由商業銀行的總準備金和流通中的現金兩部分構成，即：
B=A+C（6）
若將（2）、（3）代入（6）式中，則基礎貨幣公式為：
B=D.rd+T.rt+E+D.k（7）
再將（4）、（5）代入（7）式中，得：
B=D.rd+D.rt.t+D.e+D.k
=D.(rd+rt.t+e+k)（8）
或D=B/(rd+rt.t+e+k)（9）
其中1/(rd+rt.t+e+k)便是活期存款擴張倍數。
再將（3）代入（1），得
M1=D.k+D=D.(k+1)（10）
將（9）代入（10），則得出貨幣供應量M1的一般模式為：
（11）M1=[(k+1)/(rd+rt.t+e+k)].B
其中，B為基礎貨幣，假定貨幣乘數為m，則貨幣乘數為：
（12）m=M1/B=(k+1)/(rd+rt.t+e+k)

流通速度

貨幣流通速度是指單位貨幣在一定時期內的周轉(或實現交換)次數。
根據貨幣乘數理論其公式為：公式1（右圖）
其中，K2為廣義貨幣乘數，c為現金漏損率．rd為活期款準備金率，t為定期和儲蓄存款占活期存款的比重，rt為定期存款準備金率，e為超額準備率。

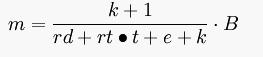結合(1)和(2)得出：公式2（右圖）
不難看出，在一定的名義GDP下，貨幣乘數B和貨幣流通速度V之間存在著反比關係，即在一定的產出水平下，貨幣流通速度增大，則貨幣乘數減少；反之亦然。所以要分析金融創新對貨幣流通速度的影響，只要找出影響貨幣乘數的因素，就可以得出相應的結論。

基礎貨幣

提到貨幣乘數，就要先從銀行的貨幣創造開始談起，而貨幣創造又要先說銀行的部分準備金制度。

銀行是以盈利為目的的企業，之所以吸收存款是要把存款以高於存款利率的價格貸出，賺的是存貸利差。所以銀行不可能把所有的錢擱在手裡，等儲戶來取錢。但也要預留一部分以防提取。這就是銀行的部分準備金制度。國家規定的有個法定準備金率記為rr，也就是銀行的準備金率不得低於這個數。

那么假設某人甲存入A銀行1000元，法定準備金率是20%，則銀行A留下200做準備金，將800貸出給乙。

乙將這800元存入銀行B，銀行B將160元留做準備金，貸出640元給丙。如此循環下去，銀行中的存款就多倍的被創造。一共是1000*1/20%(等比數列求和1000+800+640+......)當然銀行的信譽不同，面臨的提款的壓力也不同，所以部分銀行還要多放在手裡一些錢，這些超出的貨幣和銀行總資產之比就是超額準備金率，記為e，那么顯然貨幣被創造的總數就變成1000*1/(20%+e)。

當然非支票存款如活期和定期的存款和支票存款面臨的提款壓力也不一樣，那他們的法定存款準備金率也就不一樣，一般非支票存款的法定存款準備金率要低。假設非支票存款與支票存款之比為t，非支票存款的法定存款準備金率為RR，則記入非支票存款分母上要加上RR*t。而且人們不可能把所有的現金存入，而要留下部分現金，則留下的現金和支票存款之比為c的話，也稱為現金漏損率，則分母上再要加一個c。

基礎貨幣就是流通中的現金加上銀行里的準備金，記為C+R，貨幣供給M就是流通中的現金加上銀行里的支票存款(這裡指狹義貨幣M1)記為C+D，那么貨幣乘數定義為貨幣供給比上基礎貨幣記為m，則m=(C+D)/(C+R)，這裡R=D*rr(支票存款法定準備金)+D*RR*t(非支票存款的法定存款準備金)+D*e(支票存款的超額存款準備金)且C/D=c(現金漏損率)，則m=(1+c)/rr+RR*t+e+c。

由此推出狹義貨幣的貨幣乘數。中央銀行為控制貨幣供給，而在公開的市場上的業務操作來調整基礎貨幣，從而控制貨幣供給。也可以調整法定存款準備金率來調整貨幣乘數。